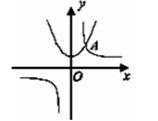
题目内容
如图,抛物线![]() 与双曲线
与双曲线![]() 相交于点A、B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A、B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
(1)求实数![]() 的值;
的值;
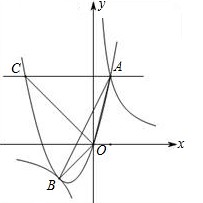
(2)过抛物线上点A作直线AC∥Ox,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.
解:(1)∵点A(1,4)在双曲线![]() 上,
上,
![]() ∴k=4.
∴k=4.
故双曲线的函数表达式为![]() .
.
设点B(t,![]() ),
),![]() ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为![]() ,则有
,则有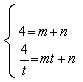
 解得
解得![]()
于是,直线AB与y轴的交点坐标为![]() ,
,
故![]()
![]() ,
,
整理得![]() ,
,
解得t=-2或![]() (舍去)
(舍去)
∴点B的坐标为(-2,-2)
∵点A,B都在抛物线![]() (a
(a![]() 0)上,
0)上,
∴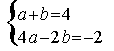 解得
解得![]()
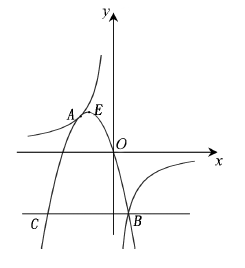
(2)如图,∵AC∥x轴,
∴C(-4,4),∴CO=![]() . 又BO=
. 又BO=![]() ,
,
![]() ∴
∴![]() .
.
设抛物线![]() (a
(a![]() 0)与x轴负半轴相交于点D,
0)与x轴负半轴相交于点D,
则点D的坐标为(-3,0).
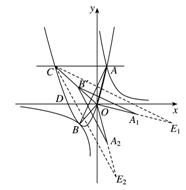
∵∠COD=∠BOD=45°,∴∠COB=90°(i)将△BOA绕点O顺时针旋转90°,得到△B’OA.这时,点B’(-2,2)是CO的中点,点A1的坐标为(4,-1).
延长OA1到点E1,使得OE1=2OA1,这时点E1(8,-2)是符合条件的点......9分
(ii)作△BOA关于x轴的对称图形△BOA2,得到点A2(1,-4);延长O A2到点E2,使得OE2=2OA2,这时点E2(2,-8)是符合条件的点
∴点E的坐标是(8,-2),或(2,-8).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
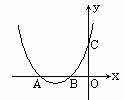
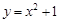 与双曲线
与双曲线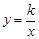 的交点A的横坐标是1,则关于
的交点A的横坐标是1,则关于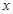 的不等式
的不等式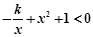 的解集是( )
的解集是( )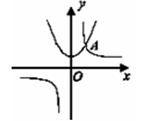
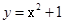 与双曲线
与双曲线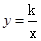 的交点A的横坐标是1,则关于
的交点A的横坐标是1,则关于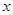 的不等式
的不等式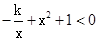 的解集是( )
的解集是( )