题目内容
【题目】阅读理解 在研究函数![]() 的图象性质时,我们用“描点”的方法画出函数的图象.
的图象性质时,我们用“描点”的方法画出函数的图象.
列出表示几组![]() 与
与![]() 的对应值:
的对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点连线:以表中各对对应值为坐标,描出各点,并用平滑的曲线顺次连接这些点,就得到函数![]() 的图象,如图1:
的图象,如图1:
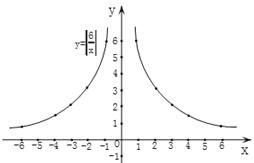
图1
可以看出,这个函数图象的两个分支分别在第一、二象限,且当![]() 时,与函数
时,与函数![]() 在第一象限的图象相同;当
在第一象限的图象相同;当![]() 时,与函数
时,与函数![]() 在第二象限的图象相同.类似地,我们把函数
在第二象限的图象相同.类似地,我们把函数![]() (
(![]() 是常数,
是常数,![]() )的图象称为“并进双曲线”.
)的图象称为“并进双曲线”.
认真观察图表,分别写出“并进双曲线”![]() 的对称性、函数的增减性性质:
的对称性、函数的增减性性质:
①图象的对称性性质: ;
②函数的增减性性质: ;
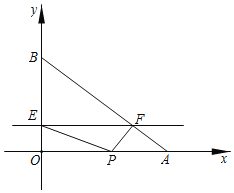
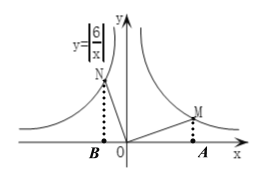
延伸探究如图2,点M,N分别在“并进双曲线”![]() 的两个分支上,
的两个分支上,![]() ,判断
,判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
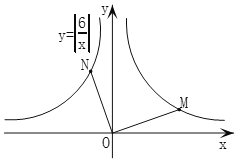
图2
【答案】阅读理解:① “并进双曲线”关于![]() 轴对称;②当
轴对称;②当![]() 时,
时,![]() 随着
随着![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随着
随着![]() 的增大而增大.延伸探究:
的增大而增大.延伸探究:![]() ,理由见解析.
,理由见解析.
【解析】
阅读理解:①设点![]() 在“并进双曲线”上可知,其关于y轴的对称点
在“并进双曲线”上可知,其关于y轴的对称点![]() 也在“并进双曲线”上,由此可知“并进双曲线”的对称性;
也在“并进双曲线”上,由此可知“并进双曲线”的对称性;
②分别根据反比例函数![]() 和
和![]() 的增减性即可得;
的增减性即可得;
延伸探究:如图(见解析),过![]() 作
作![]() 轴于
轴于![]() 点,过
点,过![]() 作
作![]() 轴于
轴于![]() 点,先利用相似三角形的性质证明
点,先利用相似三角形的性质证明![]() ,再推出
,再推出![]() ,从而根据三角形全等的性质即可得.
,从而根据三角形全等的性质即可得.
阅读理解
①设点![]() 在“并进双曲线”上
在“并进双曲线”上
则![]()
又因点![]() 关于y轴的对称点为
关于y轴的对称点为![]()
![]() ,即
,即![]() 也在“并进双曲线”上
也在“并进双曲线”上
故“并进双曲线”关于![]() 轴对称;
轴对称;
②当![]() 时,“并进双曲线”的解析式为
时,“并进双曲线”的解析式为![]() ,则
,则![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,“并进双曲线”的解析式为
时,“并进双曲线”的解析式为![]() ,则
,则![]() 随着
随着![]() 的增大而增大;
的增大而增大;
延伸探究
OM与ON的数量关系为:![]() ,理由如下:
,理由如下:
如图,过![]() 作
作![]() 轴于
轴于![]() 点,过
点,过![]() 作
作![]() 轴于
轴于![]() 点
点
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即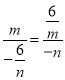
![]()
![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
![]()
![]()
在![]() 和
和![]() 中,
中,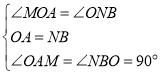
![]()
![]() .
.

练习册系列答案
相关题目