Question

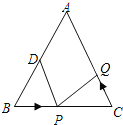
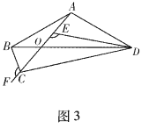
【题目】如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=．求证：CB是⊙O的切线．

Answer 1

【答案】证明见试题解析．

【解析】

试题连接OD，先证AE垂直平分BD，在直角三角形BOE中，利用锐角三角函数定义求出OE的长，由勾股定理求出BE，由OC﹣OE求出CE，再利用勾股定理求出BC，最后利用勾股定理逆定理判断即可得到BC与OB垂直，即BC为圆O的切线．

试题解析：连接OD，可得OB=OD，∵AB=AD，∴AE垂直平分BD，在Rt△BOE中，OB=3，cos∠BOE=，∴OE=，根据勾股定理得：BE==，CE=OC﹣OE=，在Rt△CEB中，BC==4，∵OB=3，BC=4，OC=5，∴，∴∠OBC=90°，即BC⊥OB，则BC为圆O的切线．