题目内容
 将5个边长都为2cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则图中重叠部分(阴影部分)的面积和为
将5个边长都为2cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则图中重叠部分(阴影部分)的面积和为
- A.8cm2
- B.6cm2
- C.4cm2
- D.2cm2
C
分析:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.即可证得:△A1EN≌△A1MF,则四边形A1MA2N的面积=四边形EA1FA2的面积= 正方形ABCD的面积.据此即可求解.
正方形ABCD的面积.据此即可求解.
解答: 解:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.
解:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.
即可证明:△A1EN≌△A1MF,
∴四边形A1MA2N的面积=四边形EA1FA2的面积= 正方形ABCD的面积.
正方形ABCD的面积.
同理可证,另外三个阴影四边形的面积都等于 正方形ABCD的面积.
正方形ABCD的面积.
∴图中重叠部分(阴影部分)的面积和=正方形ABCD的面积=4cm2.
故选C.
点评:本题主要考查了正方形的性质,正确作出辅助线,证得:四边形A1MA2N的面积=四边形EA1FA2的面积= 正方形ABCD的面积是解题的关键.
正方形ABCD的面积是解题的关键.
分析:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.即可证得:△A1EN≌△A1MF,则四边形A1MA2N的面积=四边形EA1FA2的面积=
 正方形ABCD的面积.据此即可求解.
正方形ABCD的面积.据此即可求解.解答:
 解:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.
解:在正方形ABCD中,作A1E⊥AD,A1F⊥AC.即可证明:△A1EN≌△A1MF,
∴四边形A1MA2N的面积=四边形EA1FA2的面积=
 正方形ABCD的面积.
正方形ABCD的面积.同理可证,另外三个阴影四边形的面积都等于
 正方形ABCD的面积.
正方形ABCD的面积.∴图中重叠部分(阴影部分)的面积和=正方形ABCD的面积=4cm2.
故选C.
点评:本题主要考查了正方形的性质,正确作出辅助线,证得:四边形A1MA2N的面积=四边形EA1FA2的面积=
 正方形ABCD的面积是解题的关键.
正方形ABCD的面积是解题的关键. 
练习册系列答案
相关题目
 将5个边长都为2cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则图中重叠部分(阴影部分)的面积和为( )
将5个边长都为2cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则图中重叠部分(阴影部分)的面积和为( )| A、8cm2 | B、6cm2 | C、4cm2 | D、2cm2 |
 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A、2cm2 | B、4cm2 | C、6cm2 | D、8cm2 |
 计分)
计分)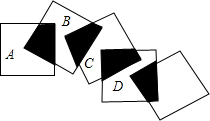 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是正方形的中心,则图中四块阴影部分的面积和为
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是正方形的中心,则图中四块阴影部分的面积和为