题目内容
【题目】取一张矩形的纸片进行折叠，具体操作过程如下： 第一步：先把矩形ABCD对折，折痕为MN，如图（1）；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得Rt△AB′E，如图（2）；
第三步：沿EB′线折叠得折痕EF，如图（3）．
若AB= 
，则EF的值是（ ）
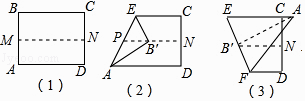
A.1
B.2
C.3
D.4
【答案】B
【解析】解：如图所示，将图3展开，可得图4， 由折叠可得，Rt△AMB'中，AM= 
AB= AB'，
∴∠AB'M=30°，
∴∠BAE=∠B'AE=30°，
∴∠EAF=60°，∠AEB=60°=∠AEB'，
∴△AEF是等边三角形，
∴EF=AE=2BE，
又∵Rt△ABE中，AB= 
，
∴BE=1，
∴EF=2，
故选：B．
根据折叠得到△AEF是等边三角形，再根据Rt△ABE中，AB= ，即可得到EF的长．
练习册系列答案
相关题目
