题目内容
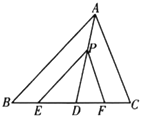
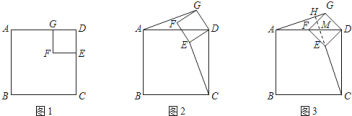
【题目】如图![]() ,若四边形
,若四边形![]() 、四边形
、四边形![]() 都是正方形,显然图中有
都是正方形,显然图中有![]() ,
,![]() ;
;
![]() 当正方形
当正方形![]() 绕
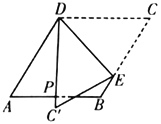
绕![]() 旋转到如图
旋转到如图![]() 的位置时,
的位置时,![]() 是否成立?若成立,请给出证明;若不成立,请说明理由;
是否成立?若成立,请给出证明;若不成立,请说明理由;
![]() 当正方形
当正方形![]() 绕
绕![]() 旋转到如图
旋转到如图![]() 的位置时,延长
的位置时,延长![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
①求证:![]() ;
;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】![]() 成立.证明见解析;(2)①证明见解析,②
成立.证明见解析;(2)①证明见解析,②![]() .
.
【解析】
(1)利用SAS证△ADG≌△CDE即可;
(2)①同样先证明△ADG≌△CDE,得出∠DAG=∠DCE,而∠DCM+∠DMC=90°,从而∠DAG+∠AMH=90°,结论显然;
②连接AC、CG,注意到DG∥AC,△GAC与△DAC的面积相等,于是考虑用等积变换,求出AG即可求出CH.
![]() 成立.
成立.
证明:∵四边形![]() 、四边形
、四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
![]() ①类似
①类似![]() 可得
可得![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
即![]() .
.
②连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,

由题意有![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴以![]() 为底边的
为底边的![]() 的高为
的高为![]() ,(延长
,(延长![]() 画高)
画高)
![]()
∴![]()
∴![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目