题目内容
16、若cosA=0.3521,则sin(90°-A)=
0.3521
.分析:先根据互为余角的三角函数关系式,得出sin(90°-A)=cosA,再将已知条件代入即可求解.
解答:解:根据互为余角的三角函数关系式,可得sin(90°-A)=cosA,
又∵cosA=0.3521,
∴sin(90°-A)=0.3521.
故答案为0.3521.
又∵cosA=0.3521,
∴sin(90°-A)=0.3521.
故答案为0.3521.
点评:本题考查了互为余角的三角函数关系式.属于基础题型,比较简单.
在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:
①一个角的正弦值等于这个角的余角的余弦值,即sinA=cos(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A).
在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:
①一个角的正弦值等于这个角的余角的余弦值,即sinA=cos(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A).

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
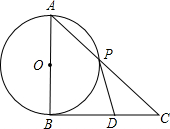 已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP.
已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP. 紧绷着的吊缆A′B′=AB.且cosA=
紧绷着的吊缆A′B′=AB.且cosA=