题目内容
已知n是大于1的整数,求证:n3可以写出两个正整数的平方差.
分析:由n3分解为(
)2•4n,4n还等于[(n+1)2-(n-1)2],得出平方差公式形式,因为n是大于1的整数,得出n(n+1),n(n-1)不仅大于1,而且均能被2整除,进一步得出原命题的正确性.
| n |
| 2 |
解答:证明:∵n3=(
)2•4n,
=(
)2[(n+1)2-(n-1)2],
=[
(n+1)]2-[
(n-1)]2,
∵n是大于1的整数,
∴n(n+1),n(n-1)不仅大于1,而且均能被2整除,
∴
(n+1),
(n-1)均为正整数,
因此,命题得证,n3可以写出两个正整数的平方差.
| n |
| 2 |
=(
| n |
| 2 |
=[
| n |
| 2 |
| n |
| 2 |
∵n是大于1的整数,
∴n(n+1),n(n-1)不仅大于1,而且均能被2整除,
∴
| n |
| 2 |
| n |
| 2 |
因此,命题得证,n3可以写出两个正整数的平方差.
点评:此题主要考查了因式分解的综合应用,n3分解出(
)2•4n,进而得出4n=[(n+1)2-(n-1)2],这是解决问题的关键.
| n |
| 2 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
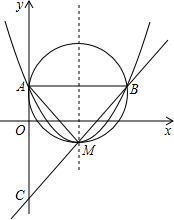 直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图)
直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图) x2-2x+k-2与x轴有两个不同的交点,与y轴交于点A,
x2-2x+k-2与x轴有两个不同的交点,与y轴交于点A,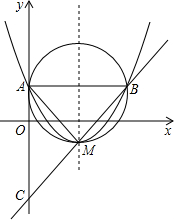 直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图)
直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图) x2-2x+k-2与x轴有两个不同的交点,与y轴交于点A,直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图)
x2-2x+k-2与x轴有两个不同的交点,与y轴交于点A,直线y2=(k-2)x+b经过抛物线的顶点M且与抛物线交于点B,与y轴交于点C(如图)