题目内容
已知n是大于3的整数，判定方程3nx2－14nx＋16n＋1＝0的两根与数2的大小关系．
答案：
解析：
解析：
|
解：这里，a＝3n，b＝－14n，＝16n＋1，k＝2． △＝b2－4ac＝(－14n)2－12n(16n＋1) ＝196n2－192n2－12n ＝4n2－12n＝4n(n－3)． ∵n＞3，∴4n(n－3)＞0， 即△＞0； ① ak2＋bk＋c＝3n×4＋(－14n)×2＋16n＋1 ＝12n－28n＋16n＋1 ＝1＞0； ② 2ak＋b＝2×3n×2＋(－14n) ＝12n－14n ＝－2n＜0． ③ 由①、②、③知，题目中的a、b、c、k适合1，因此方程3nx2－14nx＋16n＋1＝0(n＞3)的两根都大于2． |
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
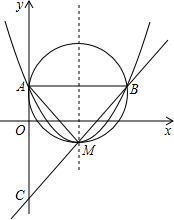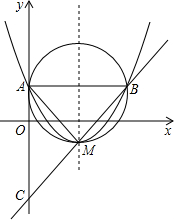直线y2=（k-2）x+b经过抛物线的顶点M且与抛物线交于点B，与y轴交于点C（如图）
x2-2x+k-2与x轴有两个不同的交点，与y轴交于点A，
直线y2=（k-2）x+b经过抛物线的顶点M且与抛物线交于点B，与y轴交于点C（如图）
x2-2x+k-2与x轴有两个不同的交点，与y轴交于点A，直线y2=（k-2）x+b经过抛物线的顶点M且与抛物线交于点B，与y轴交于点C（如图）