题目内容
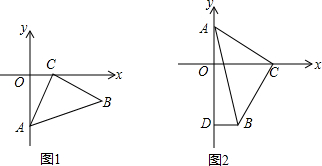
9.已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.(1)如图1,当A(0,-3),C(1,0),点B在第四象限时,则点B的坐标为(4,-1);
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断$\frac{OC+BD}{OA}$与$\frac{OC-BD}{OA}$哪一个是定值,并说明定值是多少?请证明你的结论.
分析 (1)过B作BE⊥x轴于E,推出∠2=∠OAC,∠AOC=∠BEC,根据AAS证△AOC≌△CEB,推出OA=CE,OC=BE,根据A、C的坐标即可求出答案;
(2)作BE⊥x轴于E,得出矩形OEBD,推出BD=OE,证△CEB≌△AOC,推出AO=CE,求出OC-BD=OA,代入求出即可.
解答 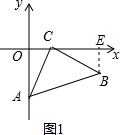 (1)解:如图1,过B作BE⊥x轴于E,
(1)解:如图1,过B作BE⊥x轴于E,
则∠BEC=∠ACB=∠AOC=90°,
∴∠1+∠2=90°,∠1+∠OAC=90°,
∴∠2=∠OAC,
在△AOC和△CEB中
∵$\left\{\begin{array}{l}{∠AOC=∠CEB}\\{∠OAC=∠2}\\{AC=BC}\end{array}\right.$,
∴△AOC≌△CEB(AAS),
∴OA=CE,OC=BE,
∵A(0,-3),C(1,0),
∴OA=CE=3,OC=BE=1,
∴OE=1+3=4,
∴点B的坐标为( 4,-1 ),
故答案为;4;
(2)结论:$\frac{OC-BD}{OA}$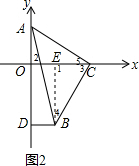 =1,
=1,
证明:如图2,作BE⊥x轴于E,
∴∠1=90°=∠2,
∴∠3+∠4=90°,
∵∠ACB=90°,
∴∠5+∠3=90°,
∴∠5=∠4,
在△CEB和△AOC中,
∵$\left\{\begin{array}{l}{∠1=∠2}\\{∠4=∠5}\\{CB=AC}\end{array}\right.$
∴△CEB≌△AOC,
∴AO=CE,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴BD∥OE,
∴四边形OEBD是矩形,
∴EO=BD,
∴OC-BD=OC-EO=CE=AO,
∴$\frac{OC-BD}{OA}$=1.
点评 本题考查了全等三角形的性质和判定,坐标与图形性质,等腰直角三角形性质,主要考查学生运用定理进行推理和计算,题目比较好.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | 60° | B. | 120° | C. | 180° | D. | 360° |

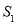 ,△ADC的面积为
,△ADC的面积为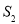 ,且
,且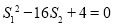 ,求△ABC的面积.
,求△ABC的面积. 如图,两个边长是2的正方形:
如图,两个边长是2的正方形:


