题目内容
已知a2+b2+c2=1且 ,求ab+bc+ac的值.
,求ab+bc+ac的值.
解:∵ ,
,
∴a-c= +
+ =
= ,
,
∵(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc),
∴ +
+ +
+ =2-2(ab+ac+bc)
=2-2(ab+ac+bc)
∴ab+ac+bc= ×(2-
×(2-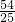 )=-
)=-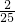 ,即ab+bc+ac的值是-
,即ab+bc+ac的值是-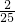 .
.
分析:根据已知条件求得a-c= ;然后由完全平方差公式求得(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc);最后将相关数据代入即可求得ab+bc+ac的值.
;然后由完全平方差公式求得(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc);最后将相关数据代入即可求得ab+bc+ac的值.
点评:本题考查了完全平方公式.解题的关键是求得a-c= .
.
 ,
,∴a-c=
 +
+ =
= ,
,∵(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc),
∴
 +
+ +
+ =2-2(ab+ac+bc)
=2-2(ab+ac+bc)∴ab+ac+bc=
 ×(2-
×(2-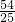 )=-
)=-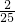 ,即ab+bc+ac的值是-
,即ab+bc+ac的值是-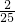 .
.分析:根据已知条件求得a-c=
 ;然后由完全平方差公式求得(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc);最后将相关数据代入即可求得ab+bc+ac的值.
;然后由完全平方差公式求得(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2(ab+ac+bc);最后将相关数据代入即可求得ab+bc+ac的值.点评:本题考查了完全平方公式.解题的关键是求得a-c=
 .
. 
练习册系列答案
相关题目