��Ŀ����
�Ķ����ϣ�������ax2+bx+c�Ķ�������ʽ������һ���֣������ȫƽ��ʽ�ķ��������䷽�����䷽���Ļ�����ʽ����ȫƽ����ʽ����д����a2��2ab+b2=��a��b��2��
���磺x2-2x+4=x2-2x+1+3=��x-1��2+
x2-2x+4=x2-4x+4+2x=��x-2��2+
x2-2x+4=
x2-2x+4+
x2=��
x-2��2+
x2
x2��x2-2x+4�����ֲ�ͬ��ʽ���䷽����������ֱ��dz����һ���������--�������ϵIJ��֣���
������Ķ����Ͻ���������⣺
��1��������������ӣ�����������ʽx2-4x+9�����ȫƽ��ʽ��ֱ��д��������ʽ����
��2����a2+3ab+b2�䷽��д������ʽ���ɣ���д�䷽���̣���
��3����֪a2+b2+c2-2ab+2c+1=0����a-b+c��ֵ��
���磺x2-2x+4=x2-2x+1+3=��x-1��2+
3
3
��x2-2x+4=x2-4x+4+2x=��x-2��2+
2x
2x
��x2-2x+4=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
������Ķ����Ͻ���������⣺
��1��������������ӣ�����������ʽx2-4x+9�����ȫƽ��ʽ��ֱ��д��������ʽ����
��2����a2+3ab+b2�䷽��д������ʽ���ɣ���д�䷽���̣���
��3����֪a2+b2+c2-2ab+2c+1=0����a-b+c��ֵ��
��������1����2�������Ķ����Ͽ��Եõ���������ʽ�е�������Ϊ��ȫƽ��ʽ������Ӷ�ȷ��������ɣ�
��3����֪��ʽ�ӿ��Ա��γɣ�a2+b2-2ab��+��c2+2c+1��=0���õ�������ȫƽ��ʽ�ĺ���0�����ɸ��������Ǹ����ĺ���0����ÿ������0�����a��b��c�Ĺ�ϵ���Ӷ���⣮
��3����֪��ʽ�ӿ��Ա��γɣ�a2+b2-2ab��+��c2+2c+1��=0���õ�������ȫƽ��ʽ�ĺ���0�����ɸ��������Ǹ����ĺ���0����ÿ������0�����a��b��c�Ĺ�ϵ���Ӷ���⣮
����⣺��1����x-2��2+5����x-3��2-2x��
��2��a2+3ab+b2=a2+3ab+��
b��2-��
b��2+b2=��a+
b��2-
b2��
a2+3ab+b2=a2+2ab+b2+ab=��a+b��2+ab��
��3����a2+b2+c2-2ab+2c+1=0��
�ࣨa2+b2-2ab��+��c2+2c+1��=0
����a-b��2+��c+1��2=0��
��a-b=0��c=-1��
��a-b+c=-1��
��2��a2+3ab+b2=a2+3ab+��
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
a2+3ab+b2=a2+2ab+b2+ab=��a+b��2+ab��
��3����a2+b2+c2-2ab+2c+1=0��
�ࣨa2+b2-2ab��+��c2+2c+1��=0
����a-b��2+��c+1��2=0��
��a-b=0��c=-1��
��a-b+c=-1��
���������⿼������ȫƽ��ʽ����ȷ������Ŀ�е��Ķ����ϣ������䷽�ķ����ǹؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
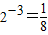 ������
������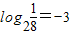 ��
��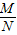 =______��a��0��a��1��M��N����������
=______��a��0��a��1��M��N����������