题目内容
5.已知a、b、c分别是△ABC的三边,且对于函数f(x)=x3-3b2x+2c3,有f(a)=f(b)=0,则△ABC是等边三角形.分析 将x=a,x=b分别代入f(x)=x3-3b2x+2c3,再化简,可得a=b=c,故可得三角形的形状.
解答 解:将x=a,x=b分别代入f(x)=x3-3bx2+2c2得:
a3-3ab2+2c3=0…①
b3-3b3+2c3=0…②
由②得2b3=2c3,
∴b=c,
∴a3-3ab2+2c3=a3-3ab2+2b3=a(a2-b2)-2b2(a-b)=(a-b)(a2-2b2+ab)=0,
∴a-b=0或a2-2b2+ab=0,
解a-b=0得a=b;
解关于a的方程a2+ba-2b2=0得a=b,
∴a=b=c,
∴三角形是等边三角形.
故答案为:等边.
点评 本题考查函数的零点,考查三角形形状的判断,考查学生分析解决问题的能力,正确理解函数的零点是关键.

练习册系列答案
相关题目
14.如果$\frac{1}{{s}_{1}}=\frac{1}{{t}_{1}}+\frac{1}{{t}_{2}}$,$\frac{1}{{s}_{2}}=\frac{1}{{t}_{1}}-\frac{1}{{t}_{2}}$,则$\frac{{s}_{1}}{{s}_{2}}$=( )
| A. | $\frac{{t}_{1}+{t}_{2}}{{t}_{2}-{t}_{1}}$ | B. | $\frac{{t}_{2}-{t}_{1}}{{t}_{2}+{t}_{1}}$ | C. | $\frac{{t}_{1}-{t}_{2}}{{t}_{2}+{t}_{1}}$ | D. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ |
15.下列运算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | |-3|=3 | C. | $\root{3}{9}$=3 | D. | $\sqrt{{(-4)}^{2}}$=-4 |
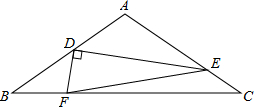 如图,在△ABC中,AB=AC,点D是AB中点,以D为直角顶点作∠EDF,分别交AC、BC于点E、F,连接EF,若tanB=$\frac{3}{4}$,BF=2,EF=3$\sqrt{5}$,则AE=5.
如图,在△ABC中,AB=AC,点D是AB中点,以D为直角顶点作∠EDF,分别交AC、BC于点E、F,连接EF,若tanB=$\frac{3}{4}$,BF=2,EF=3$\sqrt{5}$,则AE=5.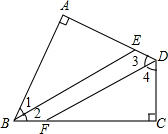 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).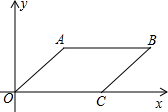 如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.
如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.