题目内容
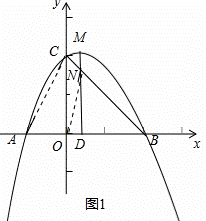
已知抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴相交于点C,该抛物线的顶点为点M,对称轴与BC相交于点N,与x轴交于点D.
(1)求该抛物线的解析式及点M的坐标;
(2)连接ON,AC,证明:∠NOB=∠ACB;
(3)点E是该抛物线上一动点,且位于第一象限,当点E到直线BC的距离为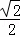 时,求点E的坐标;
时,求点E的坐标;
(4)在满足(3)的条件下,连接EN,并延长EN交y轴于点F,E、F两点关于直线BC对称吗?请说明理由.
解:(1)∵抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,
∴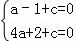 ,
,
解得 .
.
∴抛物线为y=﹣x2+x+2;
∴抛物线为y=﹣x2+x+2=﹣(x﹣ )2+
)2+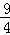 ,
,
∴顶点M( ,
,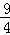 ).
).
(2)如图1,∵A(﹣1,0),B(2,0),C(0,2),
∴直线BC为:y=﹣x+2,
当x= 时,y=
时,y= ,
,
∴N( ,
, ),
),
∴AB=3,BC=2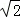 ,OB=2,BN=
,OB=2,BN= =
=
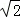 ,
,
∴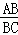 =
= =
=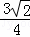 ,
, =
=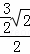 =
=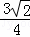 ,
,
∵∠ABC=∠NBO,
∴△ABC∽△NBO,
∴∠NOB=∠ACB;
(3)如图2,作EF⊥BC于F,
∵直线BC为y=﹣x+2,
∴设E(m,﹣m2+m+2),直线EF的解析式为y=x+b,
则直线EF为y=x+(﹣m2+2),
解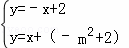 得
得 ,
,
∴F(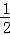 m2,﹣
m2,﹣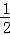 m2+2),
m2+2),
∵EF=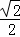 ,
,
∴(m﹣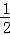 m2)2+(﹣
m2)2+(﹣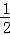 m2+2+m2﹣m﹣2)2=(
m2+2+m2﹣m﹣2)2=(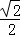 )2,
)2,
解得m=1,
∴﹣m2+m+2=2,
∴E(1,2),
(4)如图2,延长EF交y轴于Q,
∵m=1,
∴直线EF为y=x+1,
∴Q(0,1),
∵F(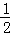 ,
, ),
),
∴FQ= =
=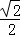 ,
,
∵EF=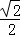 ,EF⊥BC,
,EF⊥BC,
∴E、F两点关于直线BC对称.


练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )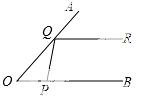
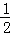 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点; 交AB,AC于点E,D,连接CE;
交AB,AC于点E,D,连接CE;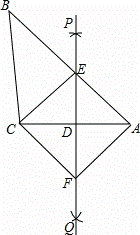

 正确的结果是( )
正确的结果是( )  B.
B. C.
C. D.
D. 
 ﹣4sin45°﹣
﹣4sin45°﹣ +
+ .
.