题目内容
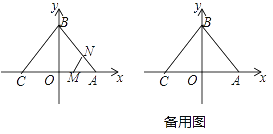
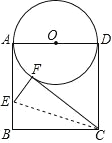
【题目】如图,正方形ABCD的边长AD为⊙O 的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则 tan∠AEF=_____.
【答案】![]()
【解析】
连接OF,OC.根据全等三角形的性质得到∠OFC=∠ODC=90°,于是得到FC是⊙O的切线;根据正方形的性质得到AD=BC=AB=CD,由∠CFE=∠B=90°,得到E,F,O三点共线.根据勾股定理得到BE的长,即可得到结论.
解:如图,连接OF,OC.
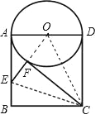
在△OCF 和△OCD 中,
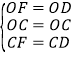 ,
,
∴△OCF≌△OCD(SSS),
∴∠OFC=∠ODC=90°,
∴CF 是⊙O 的切线,
∵四边形 ABCD 是正方形,
∴可设 AD=BC=AB=CD=2,
∵∠CFE=∠B=90°,
∴E,F,O 三点共线.
∵EF=EB,
∴在△AEO 中,AO=1,AE=2﹣BE,EO=1+BE,
∴(1+BE)2=1+(2﹣BE)2,
∴BE=![]() ,
,
∴AE=![]() ,
,
∴tan∠AEF=![]() .
.
故答案为:![]() .
.

【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.