题目内容
∠1互余∠2，∠2与∠3互补，∠1=63°，那么∠3=________．
153°
分析：根据互为余角的和等于90°先求出∠2的度数，再根据互为补角的和等于180°即可求出∠3的度数．
或根据同一个角的补角比余角大90°进行解答．
解答：∵∠1互余∠2，∠1=63°，
∴∠2=90°-63°=27°，
∵∠2与∠3互补，
∴∠3=180°-27°=153°．
或∵∠1互余∠2，∠2与∠3互补，∠1=63°，
∴∠3=90°+∠1=90°+63°=153°．
故答案为：153°．
点评：本题考查了余角与补角的定义，熟记余角的和等于90°，补角的和等于180°是解题的关键．
分析：根据互为余角的和等于90°先求出∠2的度数，再根据互为补角的和等于180°即可求出∠3的度数．
或根据同一个角的补角比余角大90°进行解答．
解答：∵∠1互余∠2，∠1=63°，
∴∠2=90°-63°=27°，
∵∠2与∠3互补，
∴∠3=180°-27°=153°．
或∵∠1互余∠2，∠2与∠3互补，∠1=63°，
∴∠3=90°+∠1=90°+63°=153°．
故答案为：153°．
点评：本题考查了余角与补角的定义，熟记余角的和等于90°，补角的和等于180°是解题的关键．
练习册系列答案
相关题目
如图，在梯形ABCD中，AD∥BC，M，N分别是AD，BC的中点，若∠B与∠C互余，则MN与BC-AD的关系是（ ）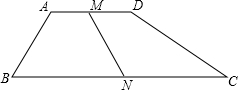
| A、2MN＜BC-AD | B、2MN＞BC-AD | C、2MN=BC-AD | D、MN=2（BC-AD） |
如图所示，点O在直线PQ上，OA是∠QOB的平分线，OC是∠POB的平分线，那么下列说法错误的是（ ）