Question

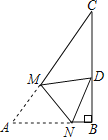
【题目】如图是集体跳绳的示意图，绳子在最高处和最低处时可以近似看作两条对称的抛物线，分别记为C1和C2，绳子在最低点处时触地部分线段CD＝2米，两位甩绳同学的距离AB＝8米，甩绳的手最低点离地面高度AE＝BN＝ 米，最高点离地AF＝BM＝米，以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系．

（1）求抛物线C1和C2的解析式；

（2）若小明离甩绳同学点A距离1米起跳，至少要跳多少米以上才能使脚不被绳子绊住？

（3）若集体跳绳每相邻两人（看成两个点）之间最小距离为0.8米，腾空后的人的最高点头顶与最低点脚底之距为1.5米，请通过计算说明，同时进行跳绳的人数最多可以容纳几人？（温馨提醒：所有同学起跳处均在直线CD上，不考虑错时跳起问题，即身体部分均在C1和C2之间才算通过），（参考数据： ＝1.414，≈1.732）

Answer 1

【答案】(1) ;(2) 至少要跳米以上才能使脚不被绳子绊住;(3) 8人．

【解析】

（1）先写出点C、D、E、F的坐标，然后设解析式代入求解即可；

（2）小明离甩绳同学点A距离1米起跳，可得此点的横坐标，代入C2解析式，即可求得；

（3）用y1减去y2，让其等于1.5，解出相应点的横坐标，求出这两个点的横坐标之间的距离，然后用间隔0.8乘以人数减1，即可解出．

解：（1）由已知得：C（﹣1，0），D（1，0），E（﹣4，），F（﹣4，），

设C2解析式为：，把代入得15a＝，

∴，

∴．

由对称性，设C1解析式，把F（﹣4，）代入得c＝，

∴

故答案为：抛物线C1和C2的解析式分别为：，．

（2）把x＝﹣3代入得，

∴至少要跳米以上才能使脚不被绳子绊住．

（3）由y1﹣y2＝1.5得：

∴，

∴x1﹣x2＝≈4×1.414＝5.656，

设同时进行跳绳的人数最多可以容纳x人

则0.8（x﹣1）≤5.656，

∴x≤8.07

∴同时进行跳绳的人数最多可以容纳8人．