题目内容
 小明在一次数学活动中,为了求
小明在一次数学活动中,为了求 | 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
1-
| 1 |
| 2n |
1-
.| 1 |
| 2n |
分析:根据图形分析,用“面积法”解题;即面积和sn=
+
+
+…+
可看作用正方形的面积减去第n个矩形的面积,为1-
.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
解答:解:由图形可得:
s1=
=1-
;
s2=
+
=
=1-
;
s3=
+
+
=
=1-
;
…;
Sn=
+
+
+…+
=1-
.
s1=
| 1 |
| 2 |
| 1 |
| 2 |
s2=
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 4 |
| 1 |
| 22 |
s3=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 7 |
| 8 |
| 1 |
| 23 |
…;
Sn=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
点评:本题考查了图形的变化类问题,重点考查学生归纳推理总结规律的能力.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
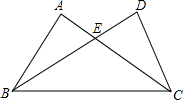 以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的概率.
以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的概率.
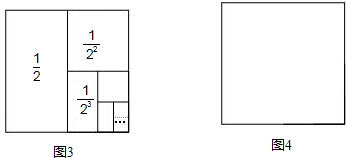

 的值,设计了如图3所示的图形.请你利用这个几何图形求
的值,设计了如图3所示的图形.请你利用这个几何图形求
 的值,设计了如图3所示的图形.请你利用这个几何图形求
的值,设计了如图3所示的图形.请你利用这个几何图形求 的值为 .
的值为 . 的值的图形.
的值的图形.
