题目内容
已知:正方形的边长为1.
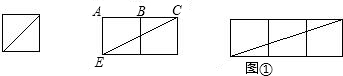
(1)如图1,可以算出一个正方形的对角线的长为 ,求两个正方形并排拼成的矩形的对角线长,并猜想出n个正方形并排拼成的矩形的对角线;
,求两个正方形并排拼成的矩形的对角线长,并猜想出n个正方形并排拼成的矩形的对角线;
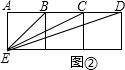
(2)根据图2,求证:△BCE∽△BED;
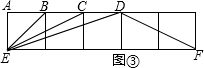
(3)由图3,在下列所给的三个结论中,选出一个正确的结论加以证明:
①∠BEC+∠BDE=45°;
②∠BEC+∠BED=45°;
③∠BEC+∠DFE=45°.

解:(1)如图1所示:
∵两个正方形拼成的矩形的长AC=2,宽AE=1
∴此时对角线EC= =
= =
=
∴同理,n个正方形组成的矩形的长为n,宽为1,
对角线长为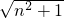 .
.
(2)如图2所示,由题意可得:BE= ,BD=2,BC=1
,BD=2,BC=1
∴ =
= =
= .
.
又∵∠CBE=∠EBD,
∴△BCE∽△BED.
(3)证明:②∠BEC+∠BED=45°.
由(2)证明出:△BCE∽△BED,
∴∠BEC=∠BDE.
由平行线定理可知:∠BDE=∠DEF,
∴∠BEC+∠BED=∠BDE+∠BED=∠DEF+∠BED=∠BEF=45°成立.
分析:(1)由于是矩形,其对角线与两边恰好构成直角三角形,利用勾股定理便可以求对角线的长.
(2)利用三角形的相似的判定定理就可求证.
(3)利用相似性求出相等的角,代替要求的角看是否正确.
点评:此题主要考查判定三角形的相似和利用相似三角形的性质求解.
∵两个正方形拼成的矩形的长AC=2,宽AE=1
∴此时对角线EC=
 =
= =
=
∴同理,n个正方形组成的矩形的长为n,宽为1,
对角线长为
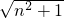 .
.(2)如图2所示,由题意可得:BE=
 ,BD=2,BC=1
,BD=2,BC=1∴
 =
= =
= .
.又∵∠CBE=∠EBD,
∴△BCE∽△BED.
(3)证明:②∠BEC+∠BED=45°.
由(2)证明出:△BCE∽△BED,
∴∠BEC=∠BDE.
由平行线定理可知:∠BDE=∠DEF,
∴∠BEC+∠BED=∠BDE+∠BED=∠DEF+∠BED=∠BEF=45°成立.
分析:(1)由于是矩形,其对角线与两边恰好构成直角三角形,利用勾股定理便可以求对角线的长.
(2)利用三角形的相似的判定定理就可求证.
(3)利用相似性求出相等的角,代替要求的角看是否正确.
点评:此题主要考查判定三角形的相似和利用相似三角形的性质求解.

练习册系列答案
相关题目
已知一个正方形的边长为a,面积为S,则( )
A、S=
| ||
| B、S的平方根是a | ||
| C、a是S的算术平方根 | ||
D、a=±
|