题目内容
20. 如图,所有正三角形的一边都与x轴平行,一顶点在y轴正半轴上,顶点依次用A1,A2,A3,A4…表示,坐标原点O到边A1A2,A4 A5,A7A8…的距离依次是1,2,3,…,从内到外,正三角形的边长依次为2,4,6,…,则A23的坐标是(8,-8).
如图,所有正三角形的一边都与x轴平行,一顶点在y轴正半轴上,顶点依次用A1,A2,A3,A4…表示,坐标原点O到边A1A2,A4 A5,A7A8…的距离依次是1,2,3,…,从内到外,正三角形的边长依次为2,4,6,…,则A23的坐标是(8,-8).
分析 根据每一个三角形有三个顶点确定出A23所在的三角形,再求出相应的三角形的边长以及A23的纵坐标的长度,即可得解.
解答 解:∵23÷3=7…2,
∴A23是第8个等边三角形的第2个顶点,
第8个等边三角形边长为2×8=16,
∴点A23的横坐标为$\frac{1}{2}$×16=8,
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,
∴点A23的纵坐标为-8,
∴点A23的坐标为(8,-8).
故答案为:(8,-8).
点评 此题考查点的坐标变化规律,主要利用了等边三角形的性质,确定出点A23所在三角形是解题的关键.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (-x5)4=x20 | C. | xm•xn=xmn | D. | x8÷x2=x4 |
5.点A(2,-5)关于x轴的对称点B的坐标为( )
| A. | (-2,5) | B. | (2,5) | C. | (-2,-5) | D. | (5,-2) |
9.下列各式能用完全平方公式分解的是( )
| A. | y2-18y+9 | B. | 4x2+6x+9 | C. | x2-8x-16 | D. | -a2+4ab-4b2 |
10.下列变形错误的是( )
| A. | 由-4x=3,得x=-$\frac{3}{4}$ | B. | 由2x=2,得x=1 | C. | 由2=-3x,得x=-$\frac{3}{2}$ | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$,得x=$\frac{1}{2}$ |
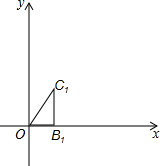 如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
 如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.
如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.