题目内容
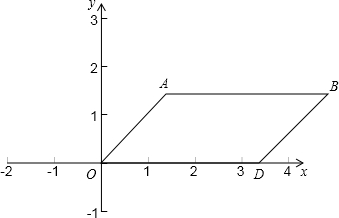
如图,在?ABDO中,已知A、D两点的坐标分别为A(| 3 |
| 3 |
| 3 |
| 3 |
(1)在图中作出四边形A′B′D′O′,并写出它的四个顶点坐标;
(2)在抛物线C上是否存在点P,使△ABP的面积恰好为四边形A′B′D′O′的面积的一半?若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)平行四边形整体向左平移,因此四点的横坐标都加减去
即可得出平移后平行四边形四顶点的坐标.
(2)先根据A′、B′、D′的坐标求出抛物线的解析式.然后求出平行四边形的面积,即可得出三角形ABP的面积,AB的长已知,那么可据此求出P点到AB的距离,也就能求出P点的纵坐标,将其代入抛物线解析式中即可求出P点的坐标.
| 3 |
(2)先根据A′、B′、D′的坐标求出抛物线的解析式.然后求出平行四边形的面积,即可得出三角形ABP的面积,AB的长已知,那么可据此求出P点到AB的距离,也就能求出P点的纵坐标,将其代入抛物线解析式中即可求出P点的坐标.
解答:解:(1)作出平移后的四边形A′B′D′O′,
顶点坐标分别为A′(0,
)、B′(2
,
)、D′(
,0)、O′(-
,0).

(2)由题意可设抛物线C的解析式为y=ax2+bx+
,
则
,
解得a=
,b=-2.
∴抛物线C的解析式为y=
x2-2x+
.
∵四边形A′B′D′O′是平行四边形,
∴它的面积为O′D′×OA′=2
×
=6.
假设存在点P,则△ABP的面积为3.
设△ABP的高为h,则
×AB×h=
×2
×h=3,
得h=
.
即点P到AB的距离为
,
∴P点的纵坐标为0或2
.
∴当P的纵坐标为0时,即有0=
x2-2x+
,
解得x1=x2=
.
当P的纵坐标为2
时,即有2
=
x2-2x+
,
解得x=
-
,x=
+
.
因此存在满足条件的点P,坐标为(
,0),(
-
,2
),(
+
,2
).
顶点坐标分别为A′(0,
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |

(2)由题意可设抛物线C的解析式为y=ax2+bx+
| 3 |
则
|
解得a=
| ||
| 3 |
∴抛物线C的解析式为y=
| ||
| 3 |
| 3 |
∵四边形A′B′D′O′是平行四边形,
∴它的面积为O′D′×OA′=2
| 3 |
| 3 |
假设存在点P,则△ABP的面积为3.
设△ABP的高为h,则
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
得h=
| 3 |
即点P到AB的距离为
| 3 |
∴P点的纵坐标为0或2
| 3 |
∴当P的纵坐标为0时,即有0=
| ||
| 3 |
| 3 |
解得x1=x2=
| 3 |
当P的纵坐标为2
| 3 |
| 3 |
| ||
| 3 |
| 3 |
解得x=
| 3 |
| 6 |
| 3 |
| 6 |
因此存在满足条件的点P,坐标为(
| 3 |
| 3 |
| 6 |
| 3 |
| 3 |
| 6 |
| 3 |
点评:本题着重考查了平行四边形的性质、待定系数法求二次函数解析式、图形面积的求法等知识点,综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 ,
,
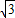 ,
, ),D(2
),D(2 ,0).将?ABDO向左平移
,0).将?ABDO向左平移 个单位,得到四边形A′B′D′O′.抛物线C经过点A′、B′、D′.
个单位,得到四边形A′B′D′O′.抛物线C经过点A′、B′、D′.
 已知如图,在平面直角坐标系中,梯形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D,若四边形ABDO的面积为4,反比例函数
已知如图,在平面直角坐标系中,梯形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D,若四边形ABDO的面积为4,反比例函数 的图象过点D,点A,则k=________.
的图象过点D,点A,则k=________.