Question

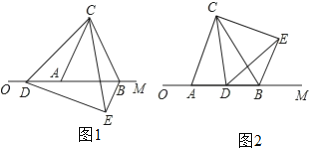
【题目】已知为等边三角形，为的高，延长至，使，连接，则__________，__________。

Answer 1

【答案】3, 120°

【解析】

根据等腰三角形和三角形外角性质求出BD＝DE，求出BC，在Rt△BDC中，由勾股定理求出BD即可．

∵△ABC为等边三角形，

∴∠ABC＝∠ACB＝60°，AB＝BC，∠DCE＝120°，

∵BD为高线，

∴∠BDC＝90°，∠DBC＝∠ABC＝30°，

∵CD＝CE，

∴∠E＝∠CDE，

∵∠E＋∠CDE＝∠ACB，

∴∠E＝30°＝∠DBC，

∵∠DCE＝120°，

∴∠CDE＝180°120°30°＝30°，

∴∠BDE＝∠BDC＋∠CDE＝120°，

∵BD是等边三角形ABC的高，CD＝1，

∴BC＝AC＝2CD＝2，

∴BE＝BC＋CE＝3，

故答案为：BE＝3，∠BDE＝120°．