题目内容
2.某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
分析 (1)设每个气排球的价格是x元,每个篮球的价格是y元,根据购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元列方程组求解即可;
(2)设购买气排球x个,则购买篮球(50-x)个,根据总费用不超过3200元,且购买气排球的个数少于30个确定出x的范围,从而可计算出最低费用.
解答 解:(1)设每个气排球的价格是x元,每个篮球的价格是y元.
根据题意得:$\left\{\begin{array}{l}{x+2y=210}\\{2x+3y=340}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$
所以每个气排球的价格是50元,每个篮球的价格是80元.
(2)设购买气排球x个,则购买篮球(50-x)个.
根据题意得:50x+80(50-x)≤3200
解得x≥26$\frac{2}{3}$,
又∵排球的个数小于30个,
∴排球的个数可以为27,28,29,
∵排球比较便宜,则购买排球越多,总费用越低,
∴当购买排球29个,篮球21个时,费用最低.
29×50+21×80=1450+1680=3130元.
点评 本题主要考查的是二元一次方程组和一元一次不等式的应用,根据题意列出方程组和不等式是解题的关键.

练习册系列答案
相关题目
10.计算(a3)2的结果是( )
| A. | a9 | B. | a6 | C. | a5 | D. | a |
14.甲、乙、丙、丁四位同学最近五次数学成绩统计如表,如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加即将举行的中学生数学竞赛,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 80 | 85 | 85 | 80 |
| 方差 | 42 | 42 | 54 | 59 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
16.下列计算中,正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (2a)3=6a3 | D. | a2b÷b=a2 |
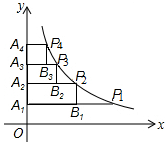 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=a,过点A1,A2,A3,A4分别作y轴的垂线,与反比例函数y=$\frac{2}{x}$(x>0)的图象相交于点P1,P2,P3,P4,过P1,P2,P3,P4分别向A1P1、A2P2、A3P3作垂线,垂足分别为B1、B2、B3,连接P1P2、P2P3、P3P4、将△B1P1P2、△B2P2P3、△B3P3P4面积分别记为S1、S2、S3,则S1+S2+S3=$\frac{3}{4}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=a,过点A1,A2,A3,A4分别作y轴的垂线,与反比例函数y=$\frac{2}{x}$(x>0)的图象相交于点P1,P2,P3,P4,过P1,P2,P3,P4分别向A1P1、A2P2、A3P3作垂线,垂足分别为B1、B2、B3,连接P1P2、P2P3、P3P4、将△B1P1P2、△B2P2P3、△B3P3P4面积分别记为S1、S2、S3,则S1+S2+S3=$\frac{3}{4}$.