题目内容
 如图,抛物线
如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a=________,点E的坐标是________.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a=________,点E的坐标是________.
 (1+
(1+ ,1+
,1+ )
)分析:把点A(3,0)代入抛物线
 即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解.
即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解.解答:把点A(3,0)代入抛物线
 ,
,解得a=
 ;
;∵四边形OABC为正方形,
∴点C的坐标为(0,3),点D的纵坐标为3,
代入y=
 x2-x-
x2-x- ,
,解得x1=1+
 ,x2=1-
,x2=1- (不合题意,舍去),
(不合题意,舍去),因此正方形BDEF的边长B为1+
 -3=
-3= -2,
-2,所以AF=3+
 -2=1+
-2=1+ ,
,由此可以得出点E的坐标为(1+
 ,1+
,1+ );
);故答案为:
 ,(1+
,(1+ ,1+
,1+ ).
).点评:此题主要结合图形与图象,利用正方形的性质以及二次函数图象上点的坐标来进行解答.

练习册系列答案
相关题目
 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.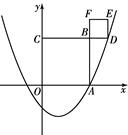
 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a=
,点E的坐标是
.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a=
,点E的坐标是
.
 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a= ,点E的坐标是 .
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a= ,点E的坐标是 .
 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a= ,点E的坐标是 .
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则a= ,点E的坐标是 .
 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.