��Ŀ����
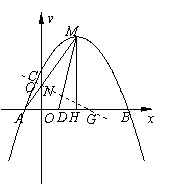
��ƽ��ֱ������ϵxOy�У���֪������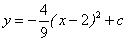 ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y����������ڵ�C���䶥��ΪM��MH��x���ڵ�H��MA��y���ڵ�N��sin��MOH��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y����������ڵ�C���䶥��ΪM��MH��x���ڵ�H��MA��y���ڵ�N��sin��MOH�� .
.
��1����������ߵĺ�������ʽ��
��2����H��ֱ����y���ཻ�ڵ�P����O��M������ֱ��PH�Ĵ��ߣ�����ֱ�ΪE��F���� 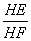 ��
�� ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
��3������1���е���������y���۵���ʹ��A���ڵ�D��������MD��QΪ��1���е��������ϵ�һ���㣬ֱ��NQ��x���ڵ�G����Q�������������˶�ʱ���Ƿ���ڵ�Q��ʹ��ANG ���ADM���ƣ������ڣ�������з���������ֱ��QG�Ľ���ʽ���������ڣ���˵������
 |
�⣺��1���� MΪ������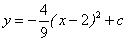 �Ķ��㣬
�Ķ��㣬
��M��2��c������OH��2��MH��|c|����a<0������������x���н��㣬��c��0����MH��c��
��sin��MOH�� ����
����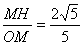 ����OM��
����OM��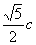 ����
����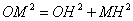 ����MH��c��4����M��2��4�����������ߵĺ�������ʽΪ��
����MH��c��4����M��2��4�����������ߵĺ�������ʽΪ��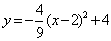 ��-----------4��
��-----------4��
��2����ͼ1����OE��PH��MF��PH��MH��OH��
���EHO����FMH����OEH����HFM�����OEH�ס�HFM��----------2��
��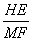 ��
��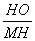 ��
�� ����
����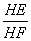 ��
�� ����MF��HF��
����MF��HF��
���OHP����FHM��45�㣮��OP��OH��2����P��0��2����
��ͼ2��ͬ���ɵã�P��0����2����-------------------------------------------2��
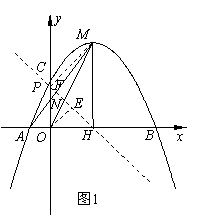

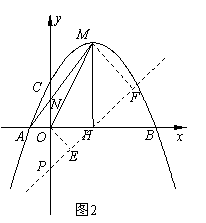

��3����A��-1��0������D��1��0����
��M��2��4����D��1��0������MD��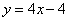 ����ON��MH�����AON�ס�AHM����
����ON��MH�����AON�ס�AHM����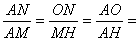
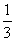 ����AN��
����AN��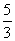 ��ON��
��ON��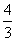 ��N��0��
��N��0��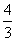 ����
����
��ͼ3������ANG �� ��AMD���ɵ�NG��MD����QG��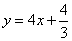 ��--------2��
��--------2��
��ͼ4������ANG �� ��ADM���ɵã�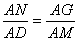 ��
��
��AG��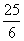 ����G��
����G��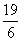 ��0������QG��
��0������QG��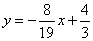 ��
��
������������������������ֱ��QG�Ľ���ʽΪ��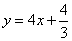 ��
��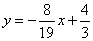 ��---2��
��---2��
 |  |

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д���֪���ε�Բ�Ľ�Ϊ60�㣬�뾶Ϊ1�������εĻ���Ϊ��������
| �� | A�� |
| B�� | �� | C�� |
| D�� |
|
Ϊ������̬��������ֹˮ����ʧ��ij��ƻ��ڽ���������ֲ���������ּס��������ֳ�����ͬ�İ�������ɹ�ѡ����������۷������£�
| ���ֳ� | ���ֳ� | ||
| ���������� | ���۵��� | ���������� | ���۵��� |
| ������1000��ʱ | 4Ԫ/�� | ������2000��ʱ | 4Ԫ/�� |
| ����1000�õIJ��� | 3.8Ԫ/�� | ����2000�õIJ��� | 3.6Ԫ/�� |
�蹺���������x�ã��������ֳ�����������÷ֱ�Ϊy����Ԫ����y����Ԫ����
��1���ô���Ҫ����1500�ð������磬�����ڼ��ֳ������������Ϊ�� ��Ԫ�����������ֳ������������Ϊ�� Ԫ��
��2���ֱ����y����y����x֮��ĺ�����ϵʽ��
��3��������Ǹô�ĸ����ˣ�Ӧ��ѡ���ļ��ֳ�����������㣬Ϊʲô��
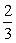 )x��3k+10��kΪż������ͼ����һ�����������ޣ���x�ᡢy��ֱ���A��B���㣬����B��һֱ����������Χ�ɵ����������Ϊ2����x���ڵ�C.
)x��3k+10��kΪż������ͼ����һ�����������ޣ���x�ᡢy��ֱ���A��B���㣬����B��һֱ����������Χ�ɵ����������Ϊ2����x���ڵ�C. ������
������
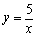 ������
����κ���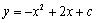 ��ͼ���ڵ�
��ͼ���ڵ� ��
��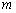 ��
��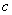 ��ֵ��
��ֵ��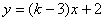 ����
���� ��
��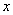 �������������
�������������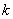 ��ֵ�����ǣ� ��
��ֵ�����ǣ� ��

