题目内容
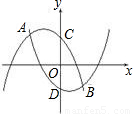
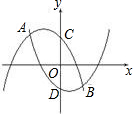 如图,抛物线F1:y1=-x2-x+1与抛物线F2:y2=x2-x-1相交于A、B两点,抛物线F1与抛物线F2分别交y轴于点C、点D
如图,抛物线F1:y1=-x2-x+1与抛物线F2:y2=x2-x-1相交于A、B两点,抛物线F1与抛物线F2分别交y轴于点C、点D
(1)判断四边形ACBD的形状为______,其面积为______;
(2)若将“抛物线F1:y1=-x2-x+1与抛物线F2:y2=x2-x-1”分别改为“抛物线F1:y1=-ax2-bx+1与抛物线F2:y2=ax2-bx-1,且(a>0)”,则四边形ACBD的形状是否发生变化?说明理由;
(3)在(2)的前提下,当b满足怎样的条件时,四边形ACBD是菱形.(直接写出答案)
解:(1)四边形ACBD是平行四边形,面积为2.(证明过程同(2).)
(2)四边形ACBD的形状不变,仍为平行四边形,理由如下:
联立F1、F2的解析式,可得:
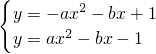 ,
,
解得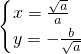 ,
,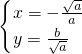 ;
;
故A(- ,
, ),B(
),B( ,-
,- );
);
易知C(0,1),D(0,-1);
则A、B,C、D都关于原点对称,
即AB、CD互相平分,
因此四边形ACBD是平行四边形;
S?ACBD= CD×|xB-xA|=
CD×|xB-xA|= ×2×
×2×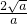 =
=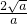 .
.
(3)若平行四边形ACBD是菱形,则AB、CD互相垂直平分,那么A、B必在x轴上,则:
- =
= =0,
=0,
即b=0;
故当b=0时,四边形ACBD是菱形.
分析:(1)(2)题的思路是一致的;根据抛物线F1、F2的解析式,可确定C(0,1)、D(0,-1);联立两个抛物线的解析式,可求得A(- ,-
,- ),B(
),B( ,
, ),由此可发现C、D以及A、B都关于原点O对称,那么AB、CD互相平分,所有四边形ACBD是平行四边形;那么它的面积可由CD与A、B横坐标差的绝对值的积的一半求得;根据这些结论即可得到(1)题的填空答案.
),由此可发现C、D以及A、B都关于原点O对称,那么AB、CD互相平分,所有四边形ACBD是平行四边形;那么它的面积可由CD与A、B横坐标差的绝对值的积的一半求得;根据这些结论即可得到(1)题的填空答案.
(3)若四边形ACBD是菱形,那么AB、CD互相垂直平分,此时A、B都在x轴上,且关于原点对称,所以A、B的纵坐标值为0,由此可求得a的值,进而可得到A、B的坐标,代入抛物线的解析式中,即可确定b的值.
点评:此题考查了二次函数的性质、函数图象交点坐标的求法、平行四边形的判定以及面积的求法、菱形的判定等知识,熟练掌握各特殊四边形的判定方法是解答此题的关键.
(2)四边形ACBD的形状不变,仍为平行四边形,理由如下:
联立F1、F2的解析式,可得:
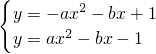 ,
,解得
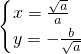 ,
,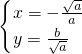 ;
;故A(-
 ,
, ),B(
),B( ,-
,- );
);易知C(0,1),D(0,-1);
则A、B,C、D都关于原点对称,
即AB、CD互相平分,
因此四边形ACBD是平行四边形;
S?ACBD=
 CD×|xB-xA|=
CD×|xB-xA|= ×2×
×2×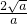 =
=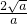 .
.(3)若平行四边形ACBD是菱形,则AB、CD互相垂直平分,那么A、B必在x轴上,则:
-
 =
= =0,
=0,即b=0;
故当b=0时,四边形ACBD是菱形.
分析:(1)(2)题的思路是一致的;根据抛物线F1、F2的解析式,可确定C(0,1)、D(0,-1);联立两个抛物线的解析式,可求得A(-
 ,-
,- ),B(
),B( ,
, ),由此可发现C、D以及A、B都关于原点O对称,那么AB、CD互相平分,所有四边形ACBD是平行四边形;那么它的面积可由CD与A、B横坐标差的绝对值的积的一半求得;根据这些结论即可得到(1)题的填空答案.
),由此可发现C、D以及A、B都关于原点O对称,那么AB、CD互相平分,所有四边形ACBD是平行四边形;那么它的面积可由CD与A、B横坐标差的绝对值的积的一半求得;根据这些结论即可得到(1)题的填空答案.(3)若四边形ACBD是菱形,那么AB、CD互相垂直平分,此时A、B都在x轴上,且关于原点对称,所以A、B的纵坐标值为0,由此可求得a的值,进而可得到A、B的坐标,代入抛物线的解析式中,即可确定b的值.
点评:此题考查了二次函数的性质、函数图象交点坐标的求法、平行四边形的判定以及面积的求法、菱形的判定等知识,熟练掌握各特殊四边形的判定方法是解答此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
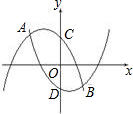 如图,抛物线F1:y1=-x2-x+1与抛物线F2:y2=x2-x-1相交于A、B两点,抛物线F1与抛物线F2分别交y轴于点C、点D
如图,抛物线F1:y1=-x2-x+1与抛物线F2:y2=x2-x-1相交于A、B两点,抛物线F1与抛物线F2分别交y轴于点C、点D

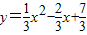 经过变换满足AC=2
经过变换满足AC=2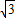 ,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值.