题目内容
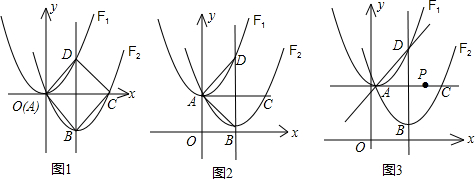
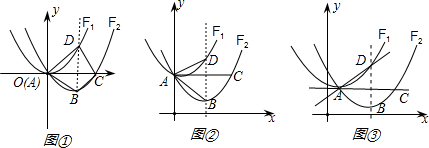
定义一种变换:平移抛物线F1得到抛物线F2,使F2经过F1的顶点A.设F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.
(Ⅰ)如图①,若F1:y=x2经过变换得到F2:y=x2+bx,点C坐标为(2,0),求抛物线F2的解析式;
(Ⅱ)如图②,若F1:y=ax2+c经过变换后点B的坐标为(2,c-1),求△ABD的面积;
(Ⅲ)如图③,若F1:y=
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 3 |
分析:(1)利用y=x2经过变换得到F2:y=x2+bx,点C坐标为(2,0),直接将C点代入即可求出;
(2)由y=ax2+c经过变换后点B的坐标为(2,c-1),根据A(0,c)在F2上,可得a=
,即可表示出△ABD的面积;
(3)求出y=
x2-
x+
的顶点坐标与对称轴,从而表示出F2的解析式,判断出四边形ABCD是菱形,要使PD+PH最小,即要使PB+PH最小,进而求出.
(2)由y=ax2+c经过变换后点B的坐标为(2,c-1),根据A(0,c)在F2上,可得a=
| 1 |
| 4 |
(3)求出y=
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
解答: 解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式,
解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式,
得b=-2,
∴F2的解析式为y=x2-2x.
(Ⅱ)∵F2:y=a(x-2)2+c-1,
而A(0,c)在F2上,可得a=
,
∴DB=(4a+c)-(c-1)=2,
∴S△ABD=2.
(Ⅲ)如图③,点C在点A的右侧,
抛物线y=
x2-
x+
,配方得y=
(x-1)2+2,
顶点坐标是A(1,2),
∵AC=2
,
∴点C的坐标为(1+2
,2).
∵F2过点A,
∴F2的解析式为y=
(x -1-
)2+1,
设AC与BD交于点N,
∴B(1+
,1),
∴D(1+
,3),
∴NB=ND=1,
∵点A与点C关于直线BD对称,
∴AC⊥DB,且AN=NC,
∴四边形ABCD是菱形.
∴AC是线段BD的垂直平分线,
∵点P在直线AC上,
∴PD=PB.
作PH⊥AD交AD于点H,则PD+PH=PB+PH.
要使PD+PH最小,即要使PB+PH最小,
此最小值是点B到AD的距离,即△ABD边AD上的高h.
∵DN=1,AN=
,DB⊥AC,
∴∠DAN=30°,故△ABD是等边三角形.
∴h=
AD=
.
∴点P到点D的距离与到直线AD的距离之和的最小值为
.
 解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式,
解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式,得b=-2,
∴F2的解析式为y=x2-2x.
(Ⅱ)∵F2:y=a(x-2)2+c-1,
而A(0,c)在F2上,可得a=
| 1 |
| 4 |
∴DB=(4a+c)-(c-1)=2,
∴S△ABD=2.
(Ⅲ)如图③,点C在点A的右侧,
抛物线y=
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 1 |
| 3 |
顶点坐标是A(1,2),
∵AC=2
| 3 |
∴点C的坐标为(1+2
| 3 |
∵F2过点A,
∴F2的解析式为y=
| 1 |
| 3 |
| 3 |
设AC与BD交于点N,
∴B(1+
| 3 |

∴D(1+
| 3 |
∴NB=ND=1,
∵点A与点C关于直线BD对称,
∴AC⊥DB,且AN=NC,
∴四边形ABCD是菱形.
∴AC是线段BD的垂直平分线,
∵点P在直线AC上,
∴PD=PB.
作PH⊥AD交AD于点H,则PD+PH=PB+PH.
要使PD+PH最小,即要使PB+PH最小,
此最小值是点B到AD的距离,即△ABD边AD上的高h.
∵DN=1,AN=
| 3 |
∴∠DAN=30°,故△ABD是等边三角形.
∴h=
| ||
| 2 |
| 3 |
∴点P到点D的距离与到直线AD的距离之和的最小值为
| 3 |
点评:此题主要考查了二次函数的图形变换与顶点坐标的求法,以及等边三角形的性质等知识,此题是近几年中考中新题型,也是数形结合的典型代表题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
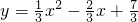 经过变换满足AC=2
经过变换满足AC=2 ,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值.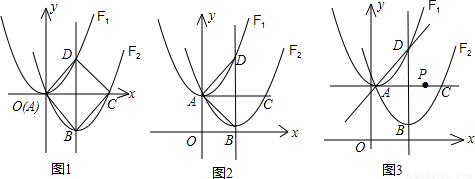
 x2-
x2- x+
x+ ,经过变换后,AC=2
,经过变换后,AC=2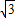 ,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.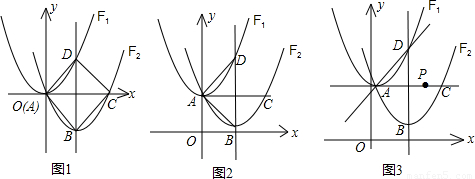
 x2-
x2- x+
x+ ,经过变换后,AC=2
,经过变换后,AC=2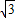 ,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.