题目内容
已知三角形的两边长是方程x2-5x+6=0的两个根,则该三角形的周长l的取值范围是 .
考点:解一元二次方程-因式分解法,三角形三边关系
专题:
分析:先解方程求出三角形的两边长,求出第三边的范围,即可求出答案.
解答:解:x2-5x+6=0,
(x-3)(x-2)=0,
x-3=0,x-2=0,
x=3,x=2,
即三角形的两边长为3和2,
设第三边为x,
则3-2<x<3+2,
∴1+3+2<x+2+3<5+3+2,
即6<l<10,
故答案为:6<l<10;
(x-3)(x-2)=0,
x-3=0,x-2=0,
x=3,x=2,
即三角形的两边长为3和2,
设第三边为x,
则3-2<x<3+2,
∴1+3+2<x+2+3<5+3+2,
即6<l<10,
故答案为:6<l<10;
点评:本题考查了解一元二次方程,三角形的三边关系定理的应用,解此题的关键是能求出三角形的第三边的范围,难度适中.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
若关于x的方程2mx-3=1的解为x=2,则m的值为( )
| A、1 | B、-1 |
| C、0.5 | D、-0.5 |
在-6,2.8,-
,48,0,-6.6,-6π,2.020020002…,
中,无理数有( )
| 1 |
| 2 |
| 22 |
| 7 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 已知:如图AD∥BC,∠C=80°,∠1=30°,求∠2,∠3的度数.
已知:如图AD∥BC,∠C=80°,∠1=30°,求∠2,∠3的度数.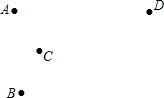 A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)
A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)