题目内容
已知两直线于交Q点,A,B,C是一直线上的三个点,L,M,N是另一直线上的三个点,且QA=AB=BC,LQ=QM=MN.求证:AL,BN,CM三线共点.
证明:如图,连MA,LC.设BN和CM交于P.
在△QBN中,QM=MN,QA=AB,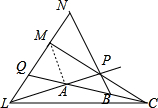
∴MA∥BN;
在△CMA中,AB=BC,BP∥MA,
∴P在BN上,P为CM的中点;
在△CML中,LQ=QM,QA= CQ,
CQ,
∴A为△CML的重心,即LA过点P.
∴BN,CM,AL三线共点.
分析:连MA,LC.设BN和CM交于P.根据中位线定理,在△QBN中,可知MA∥BN;在△CMA中,AB=BC,BP∥MA,
所以P在BN上,P为CM的中点;在△CML中,根据重心的概念和性质可证A为△CML的重心,即LA过点P.即可得证.
点评:此题考查了重心的概念和性质,同时利用了三角形的中位线定理和过一点有且只有一条直线和已知直线平行.
在△QBN中,QM=MN,QA=AB,

∴MA∥BN;
在△CMA中,AB=BC,BP∥MA,
∴P在BN上,P为CM的中点;
在△CML中,LQ=QM,QA=
 CQ,
CQ,∴A为△CML的重心,即LA过点P.
∴BN,CM,AL三线共点.
分析:连MA,LC.设BN和CM交于P.根据中位线定理,在△QBN中,可知MA∥BN;在△CMA中,AB=BC,BP∥MA,
所以P在BN上,P为CM的中点;在△CML中,根据重心的概念和性质可证A为△CML的重心,即LA过点P.即可得证.
点评:此题考查了重心的概念和性质,同时利用了三角形的中位线定理和过一点有且只有一条直线和已知直线平行.

练习册系列答案
相关题目
已知两直线![]() ,
,![]() 分别经过点A(1,0),点B
分别经过点A(1,0),点B![]() ,并且当两直线同时相交于y正半轴的点C时,恰好有
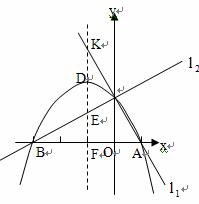
,并且当两直线同时相交于y正半轴的点C时,恰好有![]() ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线![]() 交于点K,如图所示。
交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
|
依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线![]() 绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
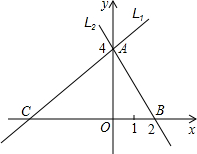 B两点,两直线相交于点A.
B两点,两直线相交于点A. ,
,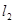 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有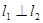 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线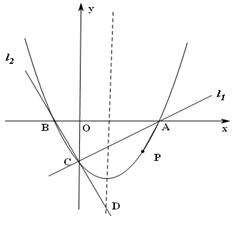
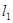 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;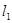 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有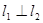 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
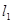 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;