题目内容
某食品加工厂准备研制加工A、B两种型号的巧克力,有关信息如下表:
| 加工一块巧克力所需的原料(克) | 加工一块巧克力所需 的费用(元) | ||
| 可可粉 | 核桃粉 | ||
| A种型号巧克力 | 13 | 4 | a |
| B种型号巧克力 | 5 | 14 | 0.8 |
(1)求表中a的值;
(2)工厂现有可可粉410克,核桃粉520克,准备利用部分原料研制加工A、B两种型号的巧克力,且B种型号的巧克力数量是A种型号的巧克力数量的一半多1,设研制加工A种型号巧克力x块(x为正整数).
①求x的取值范围;
②设加工两种巧克力的总成本为y元,求y与x的函数关系式,求y的最大值.
解:(1)24元加工A型号巧克力的数量为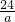 ,40元加工B型号巧克力的数量为
,40元加工B型号巧克力的数量为 ,
,
根据题意得: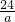 =
= ,
,
解得:a=0.48;
(2)①由研制加工A种型号巧克力x块,则研制加工B种型号巧克力( x+1)块,
x+1)块,
根据题意得: ,
,
由第一个不等式得:x≤26 ;由第二个不等式得:x≤46,
;由第二个不等式得:x≤46,
∴不等式组的解集为x≤26 ,且x为正整数;
,且x为正整数;
②根据题意得:y=0.48x+0.8( x+1)=0.88x+0.8,
x+1)=0.88x+0.8,
∵0.88>0,一次函数为增函数,
∴x取最大26时,y的最大值为23.68元.
分析:(1)先利用总钱数除以加工一块巧克力的单价得到加工巧克力的数量,分别用24元及40元表示出A型号和B型号的数量,根据题意得到两数量相等列出关于a的方程,求出方程的解即可得到a的值;
(2)①根据B种型号的巧克力数量是A种型号的巧克力数量的一半多1,由研制加工A种型号巧克力x块,表示出B型号巧克力的数量,然后根据表示出研制两种型号巧克力需要的可可粉的数量,让其小于等于410列出一个不等式,表示出两种巧克力需要的核桃粉的数量,让其小于等于520列出另一个不等式,联立两不等式,求出解集即可得到x的范围;
②根据A和B型号巧克力的一块的成本,分别乘以相应的数量,相加可得总成本,列出y与x的函数关系式,此函数为k大于0的一次函数,即为增函数,根据①求出的x的范围求出x的最大正整数值,代入一次函数解析式即可求出对应的y的最大值.
点评:此题考查了一次函数的综合运用,解决这类问题的关键是观察表格与已知,寻找题目中的相等关系或不等关系,构造出方程或不等式模型,利用有关知识来求解.同时在求一次函数y最大值时注意自变量x的取值范围.这类问题是近几年中考中的热点,一般以生活、生产、经济等问题为素材,且试题篇幅较长,信息量大,关系错综复杂,因此要求学生必须有一定的阅读理解能力,分析推理能力,数据处理能力,文字概括能力.
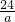 ,40元加工B型号巧克力的数量为
,40元加工B型号巧克力的数量为 ,
,根据题意得:
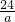 =
= ,
,解得:a=0.48;
(2)①由研制加工A种型号巧克力x块,则研制加工B种型号巧克力(
 x+1)块,
x+1)块,根据题意得:
 ,
,由第一个不等式得:x≤26
 ;由第二个不等式得:x≤46,
;由第二个不等式得:x≤46,∴不等式组的解集为x≤26
 ,且x为正整数;
,且x为正整数;②根据题意得:y=0.48x+0.8(
 x+1)=0.88x+0.8,
x+1)=0.88x+0.8,∵0.88>0,一次函数为增函数,
∴x取最大26时,y的最大值为23.68元.
分析:(1)先利用总钱数除以加工一块巧克力的单价得到加工巧克力的数量,分别用24元及40元表示出A型号和B型号的数量,根据题意得到两数量相等列出关于a的方程,求出方程的解即可得到a的值;
(2)①根据B种型号的巧克力数量是A种型号的巧克力数量的一半多1,由研制加工A种型号巧克力x块,表示出B型号巧克力的数量,然后根据表示出研制两种型号巧克力需要的可可粉的数量,让其小于等于410列出一个不等式,表示出两种巧克力需要的核桃粉的数量,让其小于等于520列出另一个不等式,联立两不等式,求出解集即可得到x的范围;
②根据A和B型号巧克力的一块的成本,分别乘以相应的数量,相加可得总成本,列出y与x的函数关系式,此函数为k大于0的一次函数,即为增函数,根据①求出的x的范围求出x的最大正整数值,代入一次函数解析式即可求出对应的y的最大值.
点评:此题考查了一次函数的综合运用,解决这类问题的关键是观察表格与已知,寻找题目中的相等关系或不等关系,构造出方程或不等式模型,利用有关知识来求解.同时在求一次函数y最大值时注意自变量x的取值范围.这类问题是近几年中考中的热点,一般以生活、生产、经济等问题为素材,且试题篇幅较长,信息量大,关系错综复杂,因此要求学生必须有一定的阅读理解能力,分析推理能力,数据处理能力,文字概括能力.

练习册系列答案
相关题目
某食品加工厂准备研制加工A、B两种型号的巧克力,有关信息如下表:
已知用24元加工A种型号巧克力的数量与用40元加工B种型号巧克力的数量相同.
(1)求表中a的值;
(2)工厂现有可可粉410克,核桃粉520克,准备利用部分原料研制加工A、B两种型号的巧克力,且B种型号的巧克力数量是A种型号的巧克力数量的一半多1,设研制加工A种型号巧克力x块(x为正整数).
①求x的取值范围;
②设加工两种巧克力的总成本为y元,求y与x的函数关系式,求y的最大值.
| 加工一块巧克力所需的原料(克) | 加工一块巧克力所需 的费用(元) | ||
| 可可粉 | 核桃粉 | ||
| A种型号巧克力 | 13 | 4 | a |
| B种型号巧克力 | 5 | 14 | 0.8 |
(1)求表中a的值;
(2)工厂现有可可粉410克,核桃粉520克,准备利用部分原料研制加工A、B两种型号的巧克力,且B种型号的巧克力数量是A种型号的巧克力数量的一半多1,设研制加工A种型号巧克力x块(x为正整数).
①求x的取值范围;
②设加工两种巧克力的总成本为y元,求y与x的函数关系式,求y的最大值.