Question

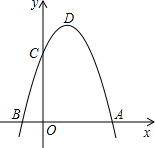如图，二次函数y=-x²+2（m-2）x+3的图象与x、y轴交于A、B、C三点，其中A（3，0），抛物线的顶点为D．
（1）求m的值及顶点D的坐标；
（2）当a≤x≤b时，函数y的最小值为1

3

4

，最大值为4，求a，b应满足的条件；
（3）在y轴右侧的抛物线上是否存在点P，使得三角形PDC是等腰三角形？如果存在，求出符合条件的点P的坐标；如果不存在，请说明理由．

Answer 1

考点：二次函数综合题

专题：

分析：（1）先把A（3，0）代入y=-x²+2（m-2）x+3，得到关于m的方程，解方程求出m的值，再利用配方法将二次函数写成顶点式，即可求出顶点D的坐标；
（2）先把y=1

3

4

代入y=-x²+2x+3，得到方程1

3

4

=-x²+2x+3，解方程求出x₁=-

1

2

，x₂=

5

2

，再利用二次函数的性质结合图象即可得出a，b应满足的条件；
（3）先求出二次函数与y轴交点C的坐标，当三角形PDC是等腰三角形时，分三种情况进行讨论：①当DC=DP时，易求点P坐标为（2，3）；②当PC=PD时，过点D作x轴的平行线，交y轴于点H，过点P作PM⊥y轴于点M，PN⊥DH于点N．由HD=HC，PC=PD，根据线段垂直平分线的判定与等腰三角形的性质得出HP平分∠MHN，再由线段垂直平分线的性质得出PM=PN．设P（m，-m²+2m+3），则m=4-（-m²+2m+3），解方程求出m的值，得出点P的坐标为(

3- 5

2

，

5+ 5

2

)或(

3+ 5

2

，

5- 5

2

)；③当CD=CP时，不符合题意．

解答：解：（1）把A（3，0）代入y=-x²+2（m-2）x+3，
得-9+6（m-2）+3=0，
解得m=3．
则二次函数为y=-x²+2x+3，
∵y=-x²+2x+3=-（x-1）²+4，
∴顶点D的坐标为（1，4）；

（2）把y=1

3

4

代入y=-x²+2x+3，
得1

3

4

=-x²+2x+3，
解得x₁=-

1

2

，x₂=

5

2

，结合图象知-

1

2

≤a≤1．
当a=-

1

2

时，1≤b≤

5

2

，
当-

1

2

＜a≤1时，b=

5

2

；

（3）x=0时，y=3，所以点C坐标为（0，3）．
当三角形PDC是等腰三角形时，分三种情况：
①如图1，当DC=DP时，
∵点P与点C关于抛物线的对称轴x=1对称，
∴点P坐标为（2，3）；
②如图2，当PC=PD时，过点D作x轴的平行线，交y轴于点H，过点P作PM⊥y轴于点M，PN⊥DH于点N．
∵HD=HC=1，PC=PD，
∴HP是线段CD的垂直平分线．
∵HD=HC，HP⊥CD，
∴HP平分∠MHN，
∵PM⊥y轴于点M，PN⊥DH于点N，
∴PM=PN．
设P（m，-m²+2m+3），则
m=4-（-m²+2m+3），解得m=

3± 5

2

，
∴P的坐标为(

3- 5

2

，

5+ 5

2

)或(

3+ 5

2

，

5- 5

2

)；
③如图3，当CD=CP时，点P在y轴左侧，不符合题意．     
综上所述，所求点P的坐标为（2，3）或(

3- 5

2

，

5+ 5

2

)或(

3+ 5

2

，

5- 5

2

)．

点评：本题是二次函数的综合题型，其中涉及到的知识点有运用待定系数法求二次函数的解析式，抛物线顶点坐标的求法，二次函数的性质，线段垂直平分线的判定与性质，等腰三角形的性质，综合性较强，难度适中．利用数形结合、分类讨论及方程思想是解题的关键．