题目内容
7．
如图，将长方形ABCD沿AE折叠，若∠BAD′比∠D′AE大17°24′，则∠D′AE的度数是24°12′．
分析 设∠D′AE=x，则∠DAE=∠D′AE=x，∠BAD′=x+17°24′，根据矩形的性质得出x+x+x+17°24′=90°，求出即可．
解答 解：设∠D′AE=x，则∠DAE=∠D′AE=x，∠BAD′=x+17°24′，
∵四边形ABCD是矩形，
∴∠DAB=90°，
∴x+x+x+17°24′=90°，
解得：x=24°12′，
即∠D′AE=24°12′．
故答案为：24°12′．
点评 本题考查了折叠的性质，矩形的性质的应用，能得出关于x的方程是解此题的关键．
练习册系列答案
相关题目
如图，画出⊙O的两条直径，依次连接这两条直径的端点，得一个四边形，判断这个四边形的形状，并说明理由．
20．圆的面积为$\frac{9}{4}$π，则60°的圆心角所对的弧长是（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{π}{2}$ | C． | $\frac{\sqrt{6}}{2}$ | D． | $\frac{π}{4}$ |
15．
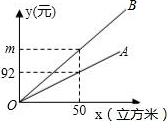某市发改委举行居民用水价格调整听证会，届时将有两个方案提供听证．如图，射线OA、射线OB分别表示现行的、方案一的每户每月的水费y（元）与每户每月的用水量x（立方米）之间的函数关系，已知方案一的用水价比现行的用水价每立方米多0.96元；
方案二如表所示，每月的每立方米用水价格由该月的用水量决定，其第一、二、三阶的用水价格之比为1：1.5：2（精确到0.01元）
（1）现行的用水量是每立方米1.84元，第三阶的用水价格a=5.22；
（2）求图中m的值和射线OB所对应的函数关系式；
（3）若小明家某月的用水量是a（立方米），请分别写出所提的两种方案下该月的水费b（元）【用含a的代数式表示】
某市发改委举行居民用水价格调整听证会，届时将有两个方案提供听证．如图，射线OA、射线OB分别表示现行的、方案一的每户每月的水费y（元）与每户每月的用水量x（立方米）之间的函数关系，已知方案一的用水价比现行的用水价每立方米多0.96元；方案二如表所示，每月的每立方米用水价格由该月的用水量决定，其第一、二、三阶的用水价格之比为1：1.5：2（精确到0.01元）
| 阶数 | 用水量（立方米） | 用水价格（元/立方米） |
| 第一阶 | 0～15（含15）的部分 | 2.61 |
| 第二阶 | 15～25（含25）的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
（2）求图中m的值和射线OB所对应的函数关系式；
（3）若小明家某月的用水量是a（立方米），请分别写出所提的两种方案下该月的水费b（元）【用含a的代数式表示】
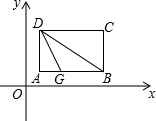如图，把矩形纸片ABCD置于直角坐标系中，AB∥x轴，BC∥y轴，AB=4，BC=3，点B（5，1）翻折矩形纸片使点A落在对角线DB上的H处得折痕DG．
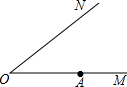如图，已知ON是一条公路桥梁，现要在上游点A处再建一座与ON平行的大桥AB，请用尺规画出AB方向（不必写作法）．并根据你的作法用一句话简单说明为什么AB和ON是平行的？
