题目内容
如图所示，球从A处射出，经球台挡板CD反射，击中球B．已知AC=10cm，BD=15cm，CD=50cm，则点E应距点C为________cm．
20
分析：根据反射定理可得∠BED=∠AEC，然后判断△BED∽△AEC，再由对应边成比例可求出EC．
解答：设CE=x，则DE=50-x，
由反射定理可得：∠BED=∠AEC，
又∵∠BDE=∠ACE=90°，
∴△BED∽△AEC，
∴
=
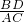，即
=
，
解得：x=20，即点E应距点C为20cm．
故答案为：20．
点评：本题考查了相似三角形的应用，解答本题的关键是判断出△BED∽△AEC，要求熟练掌握相似三角形的对应边成比例．
分析：根据反射定理可得∠BED=∠AEC，然后判断△BED∽△AEC，再由对应边成比例可求出EC．
解答：设CE=x，则DE=50-x，
由反射定理可得：∠BED=∠AEC，
又∵∠BDE=∠ACE=90°，
∴△BED∽△AEC，
∴
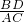=，即=，解得：x=20，即点E应距点C为20cm．
故答案为：20．
点评：本题考查了相似三角形的应用，解答本题的关键是判断出△BED∽△AEC，要求熟练掌握相似三角形的对应边成比例．
练习册系列答案
相关题目
如图所示，在台球赛中，一球在A点处，要从A射出，经球台边挡板CD反射，击中球B，已知AC=10厘米，BD=15厘米，CD=50厘米，问反射点E距点C多远才能击中球B？
如图所示，球从A处射出，经球台挡板CD反射，击中球B．已知AC=10cm，BD=15cm，CD=50cm，则点E应距点C为
