题目内容
 26、(1)如图①、图②,△ABC是等边三角形,点M是边BC上任意一点,N是BA上任意一点,且BN=CM,AM与CN相交于Q,先用量角器测量图①、图②中∠CQM的度数,并用图②证明你的猜想.
26、(1)如图①、图②,△ABC是等边三角形,点M是边BC上任意一点,N是BA上任意一点,且BN=CM,AM与CN相交于Q,先用量角器测量图①、图②中∠CQM的度数,并用图②证明你的猜想.猜想:∠CQM=
60
度.证明:
分析:根据等边三角形性质求出BC=AC,∠B=∠ACB,证△BNC≌△CMA,推出∠CAM=∠BCN,根据三角形的外角性质求出∠CQM=∠ACB即可.
解答:解:∠CQM=60°,
证明:∵等边△ACB,
∴BC=AC,∠B=∠ACB,
∵BN=CM,
∴△BNC≌△CMA,
∴∠CAM=∠BCN,
∵∠CQM=∠ACN+∠CAM=∠ACN+∠BCN=∠ACB=60°,
即∠CQM=60°,
故答案为:60.
证明:∵等边△ACB,
∴BC=AC,∠B=∠ACB,
∵BN=CM,
∴△BNC≌△CMA,
∴∠CAM=∠BCN,
∵∠CQM=∠ACN+∠CAM=∠ACN+∠BCN=∠ACB=60°,
即∠CQM=60°,
故答案为:60.
点评:本题主要考查对等边三角形性质,三角形的外角性质,全等三角形的性质和判定等知识点的理解和掌握,能求出∠CAM=∠BCN是解此题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
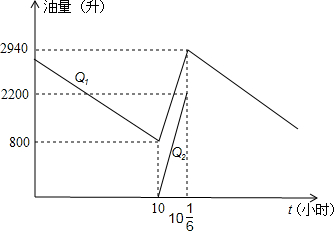 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量;

 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量;