题目内容
如图,△ABC内接⊙O,AD⊥BC,AE平分∠OAD,交外接圆于E,求证:∠BAE=∠CAE.
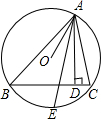
 证明:连接OE,
证明:连接OE,∵AE平分∠OAD,
∴∠OAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA.
∴∠OEA=∠DAE.
∴OE∥AD.
∵AD⊥BC,
∴OE⊥BC.
∴
 =
= .
.∴∠BAE=∠CAE.
(也可用等角的余角相等.延长AO交外接圆于F,连接BF,证明∠BAO=∠CAD;或过O做OM⊥AB于M,证明∠BAO=∠CAD.)
分析:连接OE,等腰△OAE中,∠OAE=∠OEA,而∠OAE=∠EAD,由此可证得OE∥AD,得OE⊥BC;由垂径定理可证得E是弧BC的中点,即可得到∠BAE=∠CAE相等的结论.
点评:本题考查的是垂径定理和平行线、圆周角性质.

练习册系列答案
相关题目
 5、如图,△ABC内接于⊙O,∠C=30°,AB=5,则⊙O的直径为
5、如图,△ABC内接于⊙O,∠C=30°,AB=5,则⊙O的直径为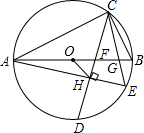 如图,△ABC内接于⊙O,AB是⊙O的直径,CD平分∠ACB交⊙O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、OH.
如图,△ABC内接于⊙O,AB是⊙O的直径,CD平分∠ACB交⊙O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、OH.
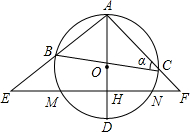 na=
na= (2012•南昌模拟)如图,△ABC内接于⊙O,点D在OC的延长线上,已知:∠B=∠CAD=30°.
(2012•南昌模拟)如图,△ABC内接于⊙O,点D在OC的延长线上,已知:∠B=∠CAD=30°.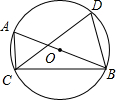 (2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是
(2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是