Question

（定义[a,b,c]为函数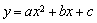的特征数,下面给出特征数为? [2m,1－m,－1－m]的函数的一些结论：

①当m＝－3时,函数图象的顶点坐标是（,）;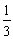

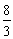②当m>0时,函数图象截x轴所得的线段长度大于;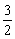

③当m<0时,函数在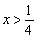时,y随x的增大而减小;

④当m≠0时,函数图象经过x轴上一个定点．

其中正确的结论有________?????? ．（只需填写序号）

 

Answer 1

【答案】

①②④．

【解析】

试题分析：因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m];

①当m=﹣3时,y=﹣6x2+4x+2=﹣6（x﹣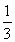）2+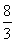,顶点坐标是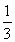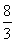（,）;此结论正确;

②当m＞0时,令y=0,有2mx2+（1﹣m）x+（﹣1﹣m）=0,解得x=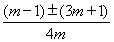,x1=1,x2=,

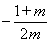|x2﹣x1|=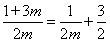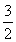＞,所以当m＞0时,函数图象截x轴所得的线段长度大于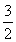,此结论正确;

③当m＜0时,y=2mx2+（1﹣m）x+（﹣1﹣m） 是一个开口向下的抛物线,其对称轴是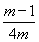：,在对称轴的右边y随x的增大而减小．因为当m＜0时,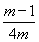=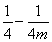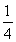＞,即对称轴在x=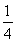右边,因此函数在x=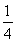右边先递增到对称轴位置,再递减,此结论错误;

④当x=1时,y=2mx2+（1﹣m）x+（﹣1﹣m）=2m+（1﹣m）+（﹣1﹣m）=0 即对任意m,函数图象都经过点（1,0）那么同样的：当m=0时,函数图象都经过同一个点（1,0）,当m≠0时,函数图象经过同一个点（1,0）,故当m≠0时,函数图象经过x轴上一个定点此结论正确．

根据上面的分析,①②④都是正确的,③是错误的．

故答案是①②④．

考点：二次函数综合题．