题目内容
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:①∠AME=108°;②![]() ;③MN=
;③MN=![]() ;④
;④![]() .其中正确结论的序号是________.
.其中正确结论的序号是________.
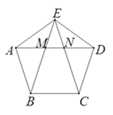
【答案】①、②、③
【解析】分析:根据正五边形的性质得到∠ABE=∠AEB=∠EAD=36°,根据三角形的内角和即可得到结论;由于∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根据等腰三角形的判定定理得到AE=AN,同理DE=DM,根据相似三角形的性质得到和AM,AN,AD有关的比例式,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3-![]() ;在正五边形ABCDE中,由于BE=CE=AD=1+
;在正五边形ABCDE中,由于BE=CE=AD=1+![]() ,得到BH=
,得到BH=![]() BC=1,根据勾股定理得到EH的值,根据三角形的面积得到结论.
BC=1,根据勾股定理得到EH的值,根据三角形的面积得到结论.
详解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°-∠EAM-∠AEM=108°,故①正确;
∵∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE
∴![]() ,
,
∴AE2=AMAD;
∴AN2=AMAD;故②正确;
∵AE2=AMAD,
∴22=(2-MN)(4-MN),
解得:MN=3-![]() ;故③正确;
;故③正确;
在正五边形ABCDE中,过E作EH⊥BC于H

∵BE=CE=AD=1+![]() ,
,
∴BH=![]() BC=1,
BC=1,
∴EH=![]() ,
,
∴S△EBC=![]() BCEH=
BCEH=![]() ×2×
×2×![]() =
=![]() ,故④错误;
,故④错误;
故答案为:①②③.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目