题目内容
 24、如图,在等腰梯形AECD中,AE∥DC,∠DAE=60°,点B是AE的中点,AC⊥CE.
24、如图,在等腰梯形AECD中,AE∥DC,∠DAE=60°,点B是AE的中点,AC⊥CE.求证:四边形ABCD是菱形.
分析:根据等腰梯形同一底上的角相等,可得∠DAB=∠E=60°,根据直角三角形斜边上的中线等于斜边的一半,可得AB=BC=BE,则易得四边形ABCD是平行四边形,即可得四边形ABCD是菱形.
解答:证明:∵四边形AECD是等腰梯形,
∴∠DAB=∠E=60°,(3分)
∵AC⊥CE,点B是AE的中点,
∴AB=BC=BE,(6分)
∴∠CBE=∠DAB=60°,(8分)
∴AD∥BC,(9分)
∵AB∥CD,
∴四边形ABCD是平行四边形,(11分)
又AB=BC,
∴四边形ABCD是菱形.(13分)
此题方法很多,添加辅助线也可,如图,只要有理有据,相应给分即可.
证法2:连接BD,(1分)
∵四边形AECD是等腰梯形,
∴∠DAB=∠E=60°,(3分)
∵AC⊥CE,点B是AE的中点,
∴AB=BC=BE,(6分)
∴△CBE是等边三角形.
∵AD=EC,
∴△ABD是等边三角形.(9分)
同理,由BD=BC,∠DBC=60°得△DBC是等边三角形,(11分)
∴AB=BC=CD=AD.
∴四边形ABCD是菱形.(13分)
(也可以证对角线互相垂直+平行四边形)
证法3:设线段AD和EC的延长线交于点F.(1分)
∵四边形AECD是等腰梯形,∠DAB=60°,
∴△AEF是等边三角形,(4分)
∵CE⊥AC,
∴FG=CE.(6分)
∵点B是AE的中点,
∴BC是△AEF的中位线且AB=BC=BE,
∴AD∥BC.(9分)
∵DC∥AB,
∴四边形ABCD是平行四边形,(11分)
又AB=BC,
∴四边形ABCD是菱形.(13分)
(也可以证四边相等)
∴∠DAB=∠E=60°,(3分)
∵AC⊥CE,点B是AE的中点,
∴AB=BC=BE,(6分)
∴∠CBE=∠DAB=60°,(8分)
∴AD∥BC,(9分)
∵AB∥CD,
∴四边形ABCD是平行四边形,(11分)
又AB=BC,
∴四边形ABCD是菱形.(13分)
此题方法很多,添加辅助线也可,如图,只要有理有据,相应给分即可.
证法2:连接BD,(1分)
∵四边形AECD是等腰梯形,
∴∠DAB=∠E=60°,(3分)
∵AC⊥CE,点B是AE的中点,
∴AB=BC=BE,(6分)
∴△CBE是等边三角形.
∵AD=EC,
∴△ABD是等边三角形.(9分)
同理,由BD=BC,∠DBC=60°得△DBC是等边三角形,(11分)
∴AB=BC=CD=AD.
∴四边形ABCD是菱形.(13分)
(也可以证对角线互相垂直+平行四边形)
证法3:设线段AD和EC的延长线交于点F.(1分)
∵四边形AECD是等腰梯形,∠DAB=60°,
∴△AEF是等边三角形,(4分)
∵CE⊥AC,
∴FG=CE.(6分)
∵点B是AE的中点,
∴BC是△AEF的中位线且AB=BC=BE,
∴AD∥BC.(9分)
∵DC∥AB,
∴四边形ABCD是平行四边形,(11分)
又AB=BC,
∴四边形ABCD是菱形.(13分)
(也可以证四边相等)
点评:此题考查了等腰梯形的性质(等腰梯形同一底上的角相等)与直角三角形的性质(直角三角形斜边上的中线等于斜边的一半)以及菱形的判定.解题时注意审题,选择适宜自己的解题方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 21、如图,在等腰梯形ABCD中,E为底BC的中点,连接AE、DE.
21、如图,在等腰梯形ABCD中,E为底BC的中点,连接AE、DE.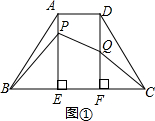 在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题:
在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题: 21、如图,在等腰梯形ABCD中,E是BC中点,连接AE、DE.
21、如图,在等腰梯形ABCD中,E是BC中点,连接AE、DE. 如图,在等腰梯形ABCD中,AD∥BC,∠B=45°,AE⊥BC于点E,AE=AD=1cm,求这个等腰梯形的腰长及面积.
如图,在等腰梯形ABCD中,AD∥BC,∠B=45°,AE⊥BC于点E,AE=AD=1cm,求这个等腰梯形的腰长及面积.