题目内容
6.已知数轴上点A表示的数为6,点B表示的数为-4,动点P表示的数为x.(1)若P沿数轴从A向左匀速运动,运动到B点时停止.
①写出线段AB的长度是10,线段PB的长度=|x+4|(填“>”、“=”或“<”);

②M为AP中点,N为PB中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请画出图形,并求出线段MN的长.
(2)当动点P在数轴这条直线上运动时;
①线段PA+PB的长度是否存在最大值或最小值,若存在,请求出这个最大值或最小值,若不存在,请说明理由;
②知识迁移:请猜想|x-1|+|x+5|的最值(最大值或最小值),并直接写出结论.
(3)动点Q从B点出发,以每秒2个单位长度的速度沿数轴匀速运动,动点P从A点出发以每秒6个单位长度向左匀速运动,若两点同时出发若干秒种后,P,Q两点相距2个单位长度,请求出x的值.
分析 (1)①根据数轴上两点之间的距离公式计算即可解决问题.
②根据中点的定义可以证明MN=$\frac{1}{2}$AB.
(2)①当动点P在数轴这条直线上运动时,线段PA+PB的长度存在最小值,不存在最大值,根据图象可以发现当点P在线段AB上PA+PB最小.
②利用①的方法可以即可解决.
(3)分两种情形:①当点Q向左运动时,②当点Q向右运动时,分别列出方程即可解决问题,注意有四种情形.
解答 解:(1)①∵点A表示的数为6,点B表示的数为-4,若P沿数轴从A向左匀速运动,运动到B点时停止,
∴AB=10,PB=|x+4|,
故答案为10,=.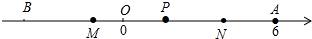
②如图所示,MN的长度不发生变化,
理由:∵BM=MP=$\frac{1}{2}$PB,PN=NA=$\frac{1}{2}$PA,
∴MN=PM+PN=$\frac{1}{2}$PB+$\frac{1}{2}$PA=$\frac{1}{2}$(PB+PA)=$\frac{1}{2}$AB=5.
(2)①当动点P在数轴这条直线上运动时,线段PA+PB的长度存在最小值,不存在最大值,
当点P在线段AB上时,PA+PB=AB=10,此时PA+PB最小.最小值为10.
②|x-1|+|x+5|的有最小值,没有最大值.
设点P表示的数为x,A表示1,B表示-5,
相当于求PA+PB的最小值,这个最小值为6.
(3)①当点Q向左运动时,由题意
(2t+10)-6t=2或6t-(2t+10)=2,
解得t=2或3,
②当点Q向右运动时,10-8t=2或8t-10=2,
解得t=1或$\frac{3}{2}$.
故两点同时出发2秒或3秒或1秒或$\frac{3}{2}$秒时,P,Q两点相距2个单位长度.
点评 本题考查一元一次方程、数轴、绝对值等知识,解题的关键是理解绝对值的几何意义,学会利用方程解决问题,属于中考常考题型.

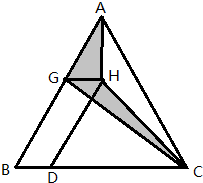 如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 内角和为360° |
| A. | y=-1 | B. | y=1 | C. | y=-3 | D. | y=3 |
 小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想.
小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想. 图中所示为一组护网的示意图,它可以看成由两组平行线组成,你能通过检验一些角得大小来判断其中的线段是否平行吗?说出你的理由.
图中所示为一组护网的示意图,它可以看成由两组平行线组成,你能通过检验一些角得大小来判断其中的线段是否平行吗?说出你的理由.