题目内容
太阳光线与地面成60°角时，一棵树的影长是5米，这棵树的高度约为 （
取1.732，精确到0.01米）
- A.2.50米
- B.8.66米
- C.10.0米
- D.4.33米
B
分析：构造直角三角形ABC，根据题意可知BC=5米，∠C=60°，在Rt△ABC中，解直角三角形求出AB的长度即可．
解答：
解：如图，在△ABC中，AB⊥BC，∠C=60°，BC=5米，
∵tan∠C=
=tan60°=，
∴AB=•AC=5≈8.66（米）．
故选B．
点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用解直角三角形的知识求出AB的长度，难度一般．
分析：构造直角三角形ABC，根据题意可知BC=5米，∠C=60°，在Rt△ABC中，解直角三角形求出AB的长度即可．
解答：
解：如图，在△ABC中，AB⊥BC，∠C=60°，BC=5米，∵tan∠C=
=tan60°=，∴AB=
•AC=5≈8.66（米）．故选B．
点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用解直角三角形的知识求出AB的长度，难度一般．
练习册系列答案
相关题目
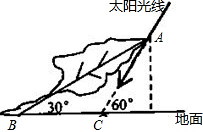如图，太阳光线与地面成60°角，一棵倾斜的大树AB与地面成30°角，这时测得大树在地面的影长BC为10m，则大树的长为（ ）m．A、5
| ||
B、10
| ||
C、15
| ||
D、20
|
如图，太阳光线与地面成60°角，一棵倾斜的大树在地面上的影长约为10米，则大树的长为
（2012•沭阳县一模）如图所示，太阳光线与地面成60°角，一棵倾斜的大树与地面成30°角，这时测得大树在地面上的影子约为10米，则大树的高约为
如图，太阳光线与地面成60°的角，照射在地面上的一只皮球上，皮球在地面上的投影长是10