题目内容
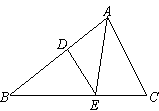
如图所示，D为△ABC中AC边上一点，AD=1，DC=2，AB=4，E是AB上一点，且△ABC的面积等于△DEC面积的2倍，则BE的长为
- A.
- B.1
- C.
- D.
B
分析：由已知AD=1，DC=2，得△DEC的面积等于△AED面积的2倍，又由△ABC的面积等于△DEC面积的2倍，得出△ABC的面积等于△BCE面积的4倍，计算△ABC的面积、△BCE面积用AB和EB为底，则两三角形的高相等，则得出BE与AB的关系，从而求出BE的长．
解答：已知AD=1，DC=2，
∴S△DEC=2S△AED，
又由S△ABC=2S△DEC，
∵S△BCE+S△AED+S△DEC=S△ABC，
∴S△BCE+S△DEC+S△DEC=2S△DEC，
∴S△BCE=S△DEC=
S△ABC，
设△ABC和△BCE的同高为h，
则：BE•h=×AB•h，
∴BE=AB=×4=1，
故选：B．
点评：此题考查的知识点是三角形的面积，关键是由已知先得出△DEC的面积等于△AED面积的2倍，然后由面积关系得出BE=AB．
分析：由已知AD=1，DC=2，得△DEC的面积等于△AED面积的2倍，又由△ABC的面积等于△DEC面积的2倍，得出△ABC的面积等于△BCE面积的4倍，计算△ABC的面积、△BCE面积用AB和EB为底，则两三角形的高相等，则得出BE与AB的关系，从而求出BE的长．
解答：已知AD=1，DC=2，
∴S△DEC=2S△AED，
又由S△ABC=2S△DEC，
∵S△BCE+S△AED+S△DEC=S△ABC，
∴S△BCE+
S△DEC+S△DEC=2S△DEC，∴S△BCE=
S△DEC=S△ABC，设△ABC和△BCE的同高为h，
则：
BE•h=×AB•h，∴BE=
AB=×4=1，故选：B．
点评：此题考查的知识点是三角形的面积，关键是由已知先得出△DEC的面积等于△AED面积的2倍，然后由面积关系得出BE=
AB． 
练习册系列答案
相关题目
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）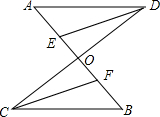
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
