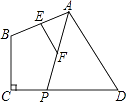
��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���ABCO�����Σ���A������Ϊ����3��4������C��x����������ϣ�ֱ��AC��y���ڵ�M��AB�߽�y���ڵ�H������BM
��1������ABCO�ı߳�
��2����ֱ��AC�Ľ���ʽ��
��3������P�ӵ�A������������ABC������2����λ/����ٶ����յ�C�����˶������PMB�����ΪS��S��0������P���˶�ʱ��Ϊt�룬
�ٵ�0��t�� ![]() ʱ����S��t֮��ĺ�����ϵʽ��
ʱ����S��t֮��ĺ�����ϵʽ��
���ڵ�P�˶������У���S=3����ֱ��д��t��ֵ��
���𰸡�
��1��5
��2��
���ı���ABCO�����Σ�
��OC=OA=AB=5����C��5��0����
��ֱ��AC�Ľ���ʽy=kx+b������ͼ�����A��C����
![]() �����
�����  ��
��
ֱ��AC�Ľ���ʽy=�� ![]() x+
x+ ![]() ��
��
��3��
��M��ֱ��BC�ľ���Ϊh��
��x=0ʱ��y= ![]() ����M��0��
����M��0�� ![]() ����HM=HO��OM=4��
����HM=HO��OM=4�� ![]() =
= ![]() ��
��
��S��ABC=S��AMB+SBMC= ![]() ABOH=
ABOH= ![]() ABHM+
ABHM+ ![]() BCh��
BCh��
![]() ��5��4=
��5��4= ![]() ��5��
��5�� ![]() +
+ ![]() ��5h�����h=
��5h�����h= ![]() ��
��
�ٵ�0��t�� ![]() ʱ��BP=BA��AP=5��2t��HM=OH��OM=
ʱ��BP=BA��AP=5��2t��HM=OH��OM= ![]() ��
��
S= ![]() BPHM=
BPHM= ![]() ��
�� ![]() ��5��2t��=��
��5��2t��=�� ![]() t��
t�� ![]() ��
��
�ڵ�2.5��t��5ʱ��BP=2t��5��h= ![]() ��
��
S= ![]() BPh=
BPh= ![]() ��
�� ![]() ��2t��5��=
��2t��5��= ![]() t��
t�� ![]() ��
��
��S=3������еĺ�������ʽ�ã�3=�� ![]() t��
t�� ![]() ��
��
��ã�t=�� ![]() ���������⣩��
���������⣩��
��S=3����ڵĽ���ʽ�ã�3= ![]() t��
t�� ![]() ��
��
��ã�t= ![]() ��
��
���������⣺��1��Rt��AOH�У�
AO= ![]() =
= ![]() =5��
=5��
�������α߳�Ϊ5��
���Դ��ǣ�5��
�����㾫�������ڱ��⿼���ȷ��һ�κ����ı���ʽ�����ε����ʣ���Ҫ�˽�ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ���������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ����ܵó���ȷ�𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�