题目内容
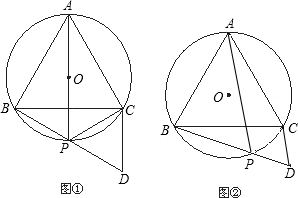
已知：如图，等边△ABC中，点D为BC边的中点，点F是AB边上一点，点E在线段DF的延长线上，∠BAE＝∠BDF，点M在线段DF上，∠ABE＝∠DBM．
（1）猜想：线段AE、MD之间有怎样的数量关系，并加以证明；
（2）在（1）的条件下延长BM到P，使MP＝BM，连接CP，若AB＝7，AE＝
，求tan∠BCP的值．
（1）猜想：
------------------------------------------1分
证明：∵ △ABC是等边三角形，点D为BC边的中点，
∴
∵ ∠BAE＝∠BDF , ∠ABE＝∠DBM
∴
∽
----------------------2分
∴
即 -------------3分
（2）解：如图， 连接EP
由（1）∽
∴
∴
∵
∴
∴
∵
∴
为等边三角形 ----------------------4分
∴
∴
∴
-----------------------5分
在Rt△AEB中，AB＝7，AE＝
∴
=
∴
-------------------6分
∵
，，∠ABE＝∠DBM
∴
∴
∴
= ---------7分解析:
略
------------------------------------------1分证明：∵ △ABC是等边三角形，点D为BC边的中点，
∴
∵ ∠BAE＝∠BDF , ∠ABE＝∠DBM
∴
∽ ----------------------2分∴
即 -------------3分（2）解：如图， 连接EP
由（1）
∽∴
∴
∵
∴
∴
∵
∴
为等边三角形 ----------------------4分∴
∴
∴
-----------------------5分在Rt△AEB中，AB＝7，AE＝
∴
= ∴
-------------------6分∵
，，∠ABE＝∠DBM∴
∴
∴
= ---------7分解析:略
练习册系列答案
阅读快车系列答案
相关题目
明理由；
已知：如图，等边△ABC的边长为6，点D、E分别在AB、AC上，且AD=AE=2，直线l过点A，且l∥BC，若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设F点运动的时间为t秒，当t＞0时，直线DF交l于点G，GE的延长线与BC的延长线交于点H，AB与GH相交于点O．
已知，如图，等边三角形ABC边长为2，以BC为对称轴将△ABC翻折，得到四边形ABDC，将此四边形放在直角坐标系xOy中，使AB在x轴上，点D在直线
已知：如图，等边△ABC的边长为2，E为BC边的中点，分别以顶点B、C为圆心，BE、CE长为半径画弧交AB、AC于点D、F．求图中阴影部分的面积．
已知：如图，等边三角形ABD与等边三角形ACE具有公共顶点A，连接CD，BE，交于点P．