题目内容
 已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
PN⊥CD于N,求证:PM=PN
证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD________
在△ABD和△CBD中
AB=CB (已知)
________
BD=BD (公共边)
∴△ABD≌△CBD________
∴________
又∵________(已知),
∴________.
角平分线的定义 ∠ABD=∠CBD SAS ∠ADB=∠CDB PM⊥ADPN⊥CD PM=PN
分析:根据角平分线的定义可得出∠ABD=∠CBD,则可证明△ABD≌△CBD,从而得出∠ADB=∠CDB,再由PM⊥AD,PN⊥CD,得出PM=PN.
解答:证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD (角平分线的定义)
在△ABD和△CBD中,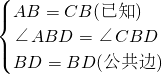 ,
,
∴△ABD≌△CBD SAS
∴∠ADB=∠CDB (全等三角形的对应角相等)
又∵PM⊥AD PN⊥CD(已知),
∴PM=PN.
故答案为:角平分线的定义,∠ABD=∠CBD,SAS,∠ADB=∠CDB,PM⊥AD PN⊥CD,PM=PN.
点评:本题考查了全等三角形的判定和性质、角平分线的定义以及角平分线的性质,是基础知识要熟练掌握.
分析:根据角平分线的定义可得出∠ABD=∠CBD,则可证明△ABD≌△CBD,从而得出∠ADB=∠CDB,再由PM⊥AD,PN⊥CD,得出PM=PN.
解答:证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD (角平分线的定义)
在△ABD和△CBD中,
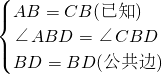 ,
,∴△ABD≌△CBD SAS
∴∠ADB=∠CDB (全等三角形的对应角相等)
又∵PM⊥AD PN⊥CD(已知),
∴PM=PN.
故答案为:角平分线的定义,∠ABD=∠CBD,SAS,∠ADB=∠CDB,PM⊥AD PN⊥CD,PM=PN.
点评:本题考查了全等三角形的判定和性质、角平分线的定义以及角平分线的性质,是基础知识要熟练掌握.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,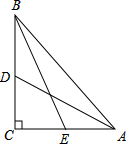 已知:(如图)在Rt△ABC中,∠C=90°,D、E分别为BC、AC的中点,AD=5,
已知:(如图)在Rt△ABC中,∠C=90°,D、E分别为BC、AC的中点,AD=5,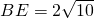 .求AB的长.
.求AB的长.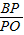 =
= ,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S,则S随a的变化而变化吗?若不变,请求出S的值;若变化,请求出S与a的关系式.
,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S,则S随a的变化而变化吗?若不变,请求出S的值;若变化,请求出S与a的关系式. =
= ,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S=______. (直接写出答案,不需证明;若S随a的变化而不变,直接写出S的值;若变化,直接写出S与a的关系式.)
,直角MPN绕顶点P旋转,角的两边分别与线段OC、OA交于点M、N(不与点C、O、A重合).设CM=a,四边形OMPN的面积为S=______. (直接写出答案,不需证明;若S随a的变化而不变,直接写出S的值;若变化,直接写出S与a的关系式.)