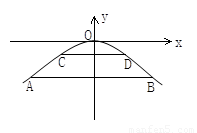题目内容
正常水位时,抛物线拱桥下的水面宽为20m,水面上升3m达到该地警戒水位时,桥下水面宽为10m.(1)在恰当的平面直角坐标系中求出水面到桥孔顶部的距离y(m)与水面宽x(m)之间的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没?

分析:(1)建立如图1所示设抛物线的解析式为y=ax2,可知点A的坐标为(10,h),则点B的坐标为(5,h+3),解出抛物线解析式,把将(
,-y)代入,可得桥孔顶部的距离y(m)与水面宽x(m)之间的函数关系式,
(2)首先求出警戒水位到桥面的距离,再求出时间t.
| x |
| 2 |
(2)首先求出警戒水位到桥面的距离,再求出时间t.
解答:解:(1)建立如图1所示设抛物线的解析式为y=ax2,(1分)

可设点A的坐标为(10,h),则点B的坐标为(5,h+3)
可得二元一次方程组:h=100a(1分)
h+3=25a(1分)
解得:a=-
,h=-4,(2分)
∴y=-
x2(1分)
将(
,-y)代入,
故桥孔顶部的距离y(m)与水面宽x(m)之间的函数关系式为:y=
x2(2分)
(2)1÷0.2=5h(1分)
答:达到警戒水位后,再过5h此桥孔将被淹没(1分)

可设点A的坐标为(10,h),则点B的坐标为(5,h+3)
可得二元一次方程组:h=100a(1分)
h+3=25a(1分)
解得:a=-
| 1 |
| 25 |
∴y=-
| 1 |
| 25 |
将(
| x |
| 2 |
故桥孔顶部的距离y(m)与水面宽x(m)之间的函数关系式为:y=
| 1 |
| 100 |
(2)1÷0.2=5h(1分)
答:达到警戒水位后,再过5h此桥孔将被淹没(1分)
点评:本题主要考查二次函数的应用,应用函数问题解决实际问题,难度适中.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目

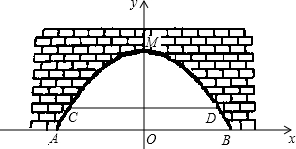 如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.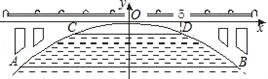
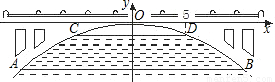
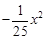 表示.在正常水位时水面AB 的宽为20m,如果水位上升3m时,水面CD的宽是10m.
表示.在正常水位时水面AB 的宽为20m,如果水位上升3m时,水面CD的宽是10m.