Question

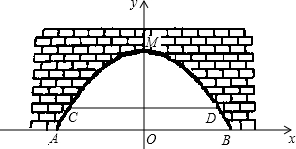如图，是某市一条河上一座古拱挢的截面图，拱桥桥洞上沿是抛物线形状，抛物线拱桥处于正常水位时水面宽AB为26m，当水位上涨1m时，抛物线拱桥的水面宽CD为24m．现以水面AB所在直线为x轴，抛物线的对称轴为y轴建立直角坐标系．
（1）求出抛物线的解析式；
（2）经过测算，水面离拱桥顶端1.5m时为警戒水位．某次洪水到来时，小明用仪器测得水面宽为10m，请你帮助小明算一算，此时水面是否超过警戒水位？

Answer 1

分析：（1）设抛物线解析式的一般形式，取对称轴为y轴，将抛物线的位置特殊化，简化抛物线解析式，根据图形选取两个点坐标求解析式；
（2）根据解析式解决实际问题．

解答：解：（1）设抛物线的解析式为
y=ax²+bx+c（a≠0），
∵对称轴为y轴，
∴y=-

b

2a

=0，
∴b=0，
∴y=ax²+c，由题意得，抛物线过点（13，0），（12，1），
把

x=13 y=0

，

x=12 y=1

，
代入得

169a+c=0 144a+c=1

，
解得

a=- 1 25 c= 169 25

，
∴抛物线的解析式为y=-

1

25

x²+

169

25

；

（2）由题意得，把x=5代入y=-

1

25

x²+

169

25

=y=-

1

25

×25+

169

25

=

144

25

，
∴点F的坐标为F（5，

144

25

），
∴MH=OM-OH=

169

25

-

144

25

=1m，
∵1m＜1.5m，
∴此时水面超过警戒水位．

点评：本题主要考查了二次函数的应用，在解题时要根据题意画出图形找出各点，再结合二次函数的知识点解出此题，这是本题的关键．