题目内容
17.先阅读,再解答:由$(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})=(\sqrt{3})^{2}-(\sqrt{2})^{2}=1$可以看出,结果中不含有二次根式.若两个含有二次根式的代数式相乘,积不含有二次根式,则称这两个代数式互为有理化因式.
在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号.
例如:
$\frac{1}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}+\sqrt{2}$
上述过程,回答下列问题:
(1)$\sqrt{3}$的有理化因式是$\sqrt{3}$,$\sqrt{2}+1$的有理化因式是$\sqrt{2}-1$
(2)化去下列式子分母中的根号:$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,$\frac{3}{3+\sqrt{6}}$=3-$\sqrt{6}$.
分析 (1)根据有理化因式的定义,仿照阅读中例子,得到$\sqrt{3}$、$\sqrt{2}$+1的有理化因式;
(2)利用分式的基本性质,分子和分母都乘以各自分母的有理化因式,化去分母中的根号.
解答 解:(1)因为$\sqrt{3}$×$\sqrt{3}$=3,所以$\sqrt{3}$的有理化因式是$\sqrt{3}$;
因为($\sqrt{2}+1$)($\sqrt{2}$-1)=3,所以$\sqrt{2}+1$的有理化因式是$\sqrt{2}$-1
故答案为:$\sqrt{3}$,$\sqrt{2}-1$
(2)$\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
$\frac{3}{3+\sqrt{6}}=\frac{3(3-\sqrt{6})}{(3+\sqrt{6})(3-\sqrt{6})}$
=3-$\sqrt{6}$
故答案为:$\frac{2\sqrt{5}}{5}$,3-$\sqrt{6}$
点评 本题考查了分母有理化的定义以及如何利用有理化因式化去分母中的根号.一般来说,$\sqrt{a}$,b$\sqrt{a}$,($\sqrt{a}$$+\sqrt{b}$)的有理化因式分别是$\sqrt{a}$,$\sqrt{a}$,($\sqrt{a}$$-\sqrt{b}$).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.三角形的内心是( )
| A. | 三边垂直平分线的交点 | B. | 三个内角角平分线的交点 | ||
| C. | 三边中线的交点 | D. | 三边高的交点 |
7.下列四个平面图形中,不能折叠成无盖的长方体盒子的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |

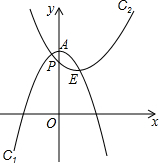 如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).
如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).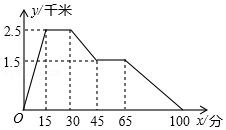 如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题:
如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题: