题目内容
满足(|x|-1)2+(|y|-1)2<2的整数对(x,y)共有多少对?
分析:利用(|x|-1)2+(|y|-1)2<2,且x,y是整数,得出(|x|-1)2=1且(|y|-1)2=0,或(|x|-1)2=0且(|y|-1)2=1,进而求出即可.
解答:解:∵(|x|-1)2+(|y|-1)2<2,且x,y是整数,
∴(|x|-1)2=1且(|y|-1)2=0,或(|x|-1)2=0且(|y|-1)2=1,
当(|x|-1)2=1,则|x|-1=±1,
解得:x=0或2或-2,
当(|y|-1)2=0,
则|y|-1=0,
解得:y=±1,
故对应点的坐标为:(0,1),(0,-1),(2,1),(2,-1),(-2,1),(-2,-1)共6对,
当(|x|-1)2=0,则|x|-1=0,
解得:x=1或-1,
当(|y|-1)2=1,
则|y|-1=±1,
解得:y=0或2或-2,
故对应点的坐标为:(1,0),(1,-2),(1,2),(-1,0),(-1,2),(-1,-2)共6对,
综上所述:满足(|x|-1)2+(|y|-1)2<2的整数对(x,y)共有12对.
∴(|x|-1)2=1且(|y|-1)2=0,或(|x|-1)2=0且(|y|-1)2=1,
当(|x|-1)2=1,则|x|-1=±1,
解得:x=0或2或-2,
当(|y|-1)2=0,
则|y|-1=0,
解得:y=±1,
故对应点的坐标为:(0,1),(0,-1),(2,1),(2,-1),(-2,1),(-2,-1)共6对,
当(|x|-1)2=0,则|x|-1=0,
解得:x=1或-1,
当(|y|-1)2=1,
则|y|-1=±1,
解得:y=0或2或-2,
故对应点的坐标为:(1,0),(1,-2),(1,2),(-1,0),(-1,2),(-1,-2)共6对,
综上所述:满足(|x|-1)2+(|y|-1)2<2的整数对(x,y)共有12对.
点评:此题主要考查了绝对值的性质,利用绝对值的性质以及整数的性质得出x,y的值是解题关键.

练习册系列答案
相关题目
满足(n2-n-1)n+2=1的整数n有几个( )
| A、4个 | B、3个 | C、2个 | D、1个 |
满足不等式-1<
≤2的整数解的个数是( )
| 1-2x |
| 3 |
| A、5 | B、4 | C、3 | D、无数个 |
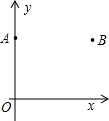 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8 ).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8 ).