题目内容
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,点
,点![]() 在第二象限.
在第二象限.
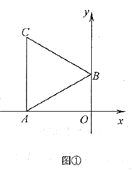
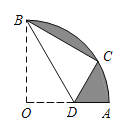
(Ⅰ)如图①,求点![]() 的坐标;
的坐标;
(Ⅱ)将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 旋转后的对应点为
旋转后的对应点为![]() .
.
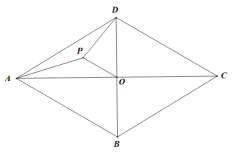
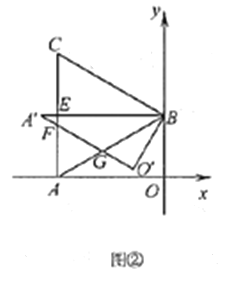
①如图②,当旋转角为30°时,![]() 与
与![]() 分别交于点
分别交于点![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 公共部分面积
公共部分面积![]() 的值;
的值;
②若![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 长的取值范围(直接写出结果即可).
长的取值范围(直接写出结果即可).
【答案】(Ⅰ)点![]() 的坐标为
的坐标为![]() ;(Ⅱ)①
;(Ⅱ)①![]() ;②
;②![]() .
.
【解析】
(Ⅰ)利用![]() 的坐标,求解
的坐标,求解![]() 利用等边三角形的性质可得答案;
利用等边三角形的性质可得答案;
(Ⅱ) ①过点![]() 作
作![]() 于点
于点![]() ,分别求解
,分别求解![]() ,
,![]() 的面积,利用
的面积,利用![]() ,可得答案;②如图,
,可得答案;②如图,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上运动,延长
为半径的圆上运动,延长![]() 至
至![]() ,使
,使![]() 则
则![]() 设
设![]() ,得到:
,得到:![]()
![]() 所以:
所以:![]() 表示点
表示点![]() 与
与![]() 之间的距离,连接
之间的距离,连接![]() 交圆
交圆![]() 于
于![]() ,当
,当![]() 在
在![]() 的下方,
的下方,![]() 最短,反之最长,从而可得答案.
最短,反之最长,从而可得答案.
解:(Ⅰ)![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)①过点![]() 作
作![]() 于点
于点![]() ,
,
∵将![]() 顺时针旋转30°,得
顺时针旋转30°,得![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
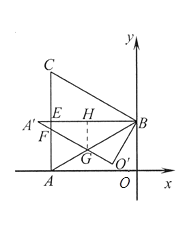
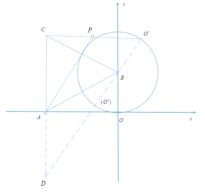
②如图,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上运动,
为半径的圆上运动,
延长![]() 至
至![]() ,使
,使![]() 则
则![]()
设![]() ,则由勾股定理得:
,则由勾股定理得:![]()
![]()
![]() 为
为![]() 的中点,
的中点,
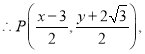
![]()
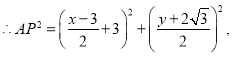
![]()
所以:![]() 表示点
表示点![]() 与
与![]() 之间的距离,连接
之间的距离,连接![]() 交圆
交圆![]() 于
于![]() ,
,
当![]() 在
在![]() 的下方,
的下方,![]() 最短,反之最长,
最短,反之最长,
设![]() 为
为![]()
![]()
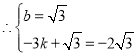
解得: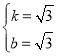
![]() 为:
为:![]()
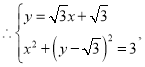
解得: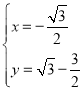 或
或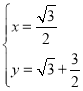
![]() 当
当![]() 在
在![]() 的下方时,坐标为:
的下方时,坐标为:
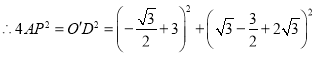
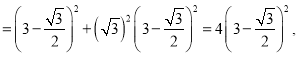
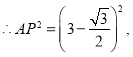
![]()
![]()
同理:当![]() 在
在![]() 的上方时,
的上方时,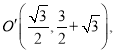
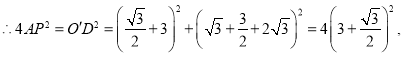
![]()
![]()
![]()

练习册系列答案
相关题目