题目内容
【题目】综合与实践
动手操作:
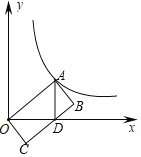
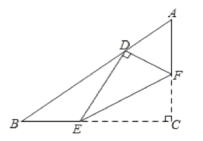
第一步:如图1,正方形纸片ABCD沿对角线AC所在直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一直线上,折痕分别为CE,CF.如图2.
第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3
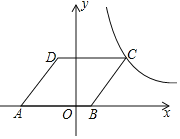
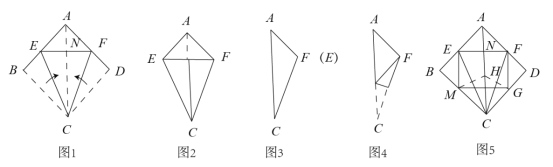
第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的虚线为折痕.
问题解决:
(1)在图5中,∠BEC的度数是 ,![]() 的值是 ;
的值是 ;
(2)在图5中,请判断四边形EMGF的形状,并说明理由;
(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .
【答案】(1)67.5°;![]() ;(2)四边形EMGF是矩形,理由见解析;(3)菱形FGCH或菱形EMCH(一个即可).
;(2)四边形EMGF是矩形,理由见解析;(3)菱形FGCH或菱形EMCH(一个即可).
【解析】
(1)由正方形的性质可得∠B=90°,∠ACB=∠BAC=45°,根据折叠的性质可得∠BCE =22.5°,继而可求得∠BEC=67.5°,在Rt△AEN中,由sin∠EAN=![]() 可得AE=
可得AE=![]() EN,即可求得
EN,即可求得![]() ;
;
(2)四边形EMGF是矩形,理由如下:由折叠的性质可得∠1=∠2=∠3=∠4=22.5°,CM=CG,∠BEC=∠NEC=∠NFC=∠DFC=67.5°,MC=ME,GC=GF,∠5=∠1=22.5°,∠6=∠4=22.5°,继而可得∠MEF=∠GFE=90°,再根据等腰直角三角形的性质可得 ∠CMG=45°,由三角形外角的性质得∠BME=∠1+∠5=45°,根据平角的定义求得∠EMG=90°,根据有三个角是直角的四边形是矩形即可得到四边形EMGF是矩形;
(3) 如图所示,四边形EMCH是菱形,理由如下:先证明四边形EMCH是平行四边形,再根据有一组邻边相等的平行四边形是菱形即可证明平行四边形EMCH是菱形.(同理四边形FGCH也是菱形).
(1)∵四边形ABCD是正方形,
∴∠B=90°,∠ACB=![]() ∠BCD=45°,∠BAC=
∠BCD=45°,∠BAC=![]() ∠BAD=45°,
∠BAD=45°,
∵折叠,
∴∠BCE=![]() ∠BCE=22.5°,BE=EN,∠ENC=∠B=90°,
∠BCE=22.5°,BE=EN,∠ENC=∠B=90°,
∴∠BEC=90°-22.5°=67.5°,∠ANE=90°,
在Rt△AEN中,sin∠EAN=![]() ,
,
∴![]() ,
,
∴AE=![]() EN,
EN,
∴![]() ,
,
故答案为:67.5°,![]() ;
;
(2)四边形EMGF是矩形,理由如下:
∵四边形ABCD是正方形,∴∠B=∠BCD=∠D=90°,
由折叠可知:∠1=∠2=∠3=∠4=22.5°,CM=CG,
∠BEC=∠NEC=∠NFC=∠DFC=67.5°,
由折叠可知:MH、GH分别垂直平分EC,FC,
∴MC=ME,GC=GF,
∴∠5=∠1=22.5°,∠6=∠4=22.5°,
∴∠MEF=∠GFE=90°,
∵∠MCG=90°,CM=CG,
∴∠CMG=45°,
又∵∠BME=∠1+∠5=45°,
∴∠EMG=180°-∠CMG-∠BME=90°,
∴四边形EMGF是矩形;

(3) 如图所示,四边形EMCH是菱形,理由如下:

由(2)∠BME=45°=∠BCA,
∴EM//AC,
∵折叠,
∴CM=CH,EM=CM,
∴EM=CH,
∴EM![]() CH,
CH,
∴四边形EMCH是平行四边形,
又CM=EM,
∴平行四边形EMCH是菱形.
(同理四边形FGCH是菱形,如图所示
 ).
).

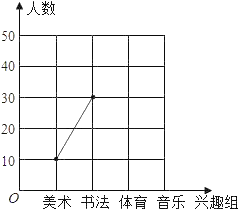
【题目】某校计划开设美术、书法、体育、音乐兴趣班,为了解学生报名的意向,随机调查了部分学生,要求被调查的学生必选且只选一项,根据调查结果绘制出如下不完整的统计图表:
兴趣班 | 人数 | 百分比 |
美术 | 10 |
|
书法 | 30 |
|
体育 |
|
|
音乐 | 20 |
|
根据统计图表的信息,解答下列问题:
(1)直接写出本次调查的样本容量和表中![]() 的值;
的值;
(2)将折线图补充完整;
(3)该校现有2000名学生,估计该校参加音乐兴趣班的学生有多少人?